À l’occasion de Devoxx 2023, Meritis a organisé un concours de code en ligne : Code on Time créé par Gaëtan Eleouet, Ingénieur Software-Engineering, Expert Java Meritis. Le principe : résoudre 4 exercices de code le plus efficacement possible depuis son ordinateur. Du 19 au 27 avril dernier, 332 développeurs de tous les niveaux ont participé. Découvrez les réponses du gagnant de Code On time ainsi que quelques astuces de résolution pour vous permettre de relever le prochain défi.
Pour remporter l’épreuve, il fallait non seulement donner une bonne réponse mais aussi tenter de récolter le plus de points pour gagner une PS5 !
Rédouane ELGHAZI présente ci-dessous des éléments d’optimisation. Et le gagnant Nonered vous explique ses éléments de résolution pour exercice d’optimisation.
Si vous souhaitez continuer à vous entraîner, revoir ou améliorer vos réponses, augmenter ton score… c’est encore possible !

1er exercice : le déploiement des chronobots.
Le sujet nous demande de trouver la ligne sur laquelle il y a le plus grand nombre.
Il faut trouver la position de la plus grande valeur.
On peut procéder en trouvant la plus grande valeur puis sa position.
L’objectif de cet exercice est de familiariser le joueur avec le système de lecture des entrées et de soumission de la solution. Pourtant, un piège était présent avec l’indexation à 1 des lignes (peu courant)
2e exercice : une pléthore de chronobots
Le sujet est beaucoup sérieux et introduit le protocole des chronobots. On cherche le nombre maximal de missions qui se superposent, c’est-à-dire qu’elles nécessitent chacune n chronobot différent pour être effectuée.
La difficulté est ici accentuée par la taille du jeu de données qui n’autorise que « péniblement » des algorithmes peu optimums.
Comment compter le nombre de missions à chaque instant ?
La résolution de cette question va se faire en deux passes, tout d’abord dans un tableau de taille tmax nous allons inscrire (+1) et (-1) à chaque début et fin de mission.
Une seconde passe va faire la somme cumulée des valeurs du tableau.
Ainsi, le tableau contient à chaque instant le nombre de missions à cet instant, il suffit alors d’en prendre le max.
On retrouve cette façon de faire dans les questions sur le nombre de parenthèses ouvertes dans une expression ?
3e exercice : Docteur du temps
Avec un clin d’œil à une série britannique, cet exercice est un peu trompeur, ce n’est pas réellement un exercice d’optimisation, malgré le format de résultat attendu.
On demande de trouver les missions que doit effectuer un « docteur » pour maximiser son revenu. Le problème est que choisir de faire une mission A qui rapporte beaucoup à un instant peut rendre impossible à effectuer la mission qui rapportait pourtant énormément ! C’est un problème de programmation dynamique !
Une fois la classe de problème reconnue, la résolution est assez simple, pour chaque instant, on va retenir la somme maximum atteinte.
On trie les missions par heure de début et l’on va mettre à jour le tableau à l’heure de fin de la mission. La difficulté est d’aller chercher la valeur maximum atteinte au début sans reparcourir l’ensemble du tableau.
On peut retenir ce maximum et sa position et ne parcourir que les cases manquantes.
Le maximum est ainsi construit en remontant la liste de max depuis la dernière mission.
Malgré le format proposé, la solution optimale est aisément atteignable et a été fixée par construction à 1 million ?
Pour en savoir plus sur la programmation dynamique, une conférence du devfest Nantes en explique les concepts.
4e exercice : LE vrai exercice d’optimisation !
On cherche comme à l’exercice précédent à choisir les missions à effectuer, mais il y a plein de chronobots et une notion d’obsolescence a été introduite.
Une première approche est un « glouton », pour chaque chronobot, on effectue la première mission disponible. On peut l’améliorer avec l’algorithme de l’exercice 3.
Un des jeux de données a une particularité, ils sont plus efficaces après leur « obsolescence », l’algorithme trop générique pourrait sous-performer ici.
Enfin, le maximum de points était sur le jeu de données 3, et je laisse Yoan le gagnant nous décrire son approche.
Solution de Nanored4498
L’idée va être de prendre les chronobots un par un et de leur assigner les missions qu’ils doivent faire. Pour cela, on distinguera deux cas : c > 100 et c⩽ 100. Considérons maintenant un chronobot dont le temps avant obsolescence est o le coût de réparation e et le « coefficient de gain de récompense » c. Les missions sont données par des quadruplets (d, f , r, l) avec d, le début de la mission, fsa fin, rsa récompense et l, a longueur. Initialement lest donné par f− d. À noter que par la suite je ré-indexe les temps d et f de sorte à ce que toutes ces valeurs soient comprises entre 0 et 2n où n est le nombre de missions (d’où l’importance de stocker au préalable la longueur l qui ne peut alors plus être retrouvé). Je note aussi M l’ensemble des missions qui n’ont toujours pas été assignées à un chronobot.
1. c > 100
Avant l’obsolescence Pour le cas c > 100, on peut supposer que plus on rentre en obsolescence tôt, mieux c’est, car les missions suivantes rapporteront plus de points. Comme il a dû être trouvé au troisième problème du challenge, il est possible de faire de la programmation dynamique pour choisir les missions qui rapporteront le plus de points jusqu’à un certain temps t. Dans mon code, je note dp[t] le score maximal qui peut être obtenu par un chronobot en ne prenant que des missions dont la fin est inférieure ou égale à t et pred [t] l’indice de la dernière mission à effectuer pour obtenir ce score ou −1 si dp[t] vaut 0. On dispose alors de la relation :
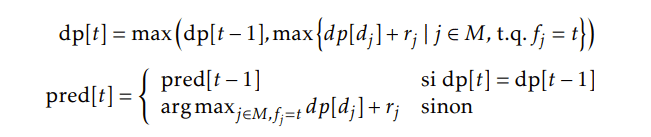
On peut désormais rajouter le calcul de somme des longueurs des tâches qui donne le meilleur score jusqu’au temps t. Notons le L[t] :
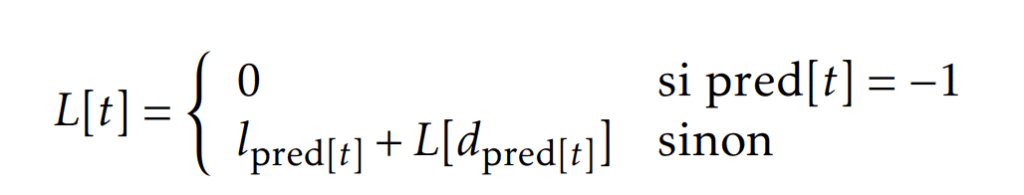
Lorsque pour un certain temps t0, on obtient L[t0] > o alors on arrête la programmation dynamique et on assigne toutes les missions de la solution optimale trouvée jusqu’au temps t au chronobot actuel. À noter qu’il faut désormais mettre à jour nos relations de récurrence, car la dernière mission sélectionnée se finira après l’obsolescence :
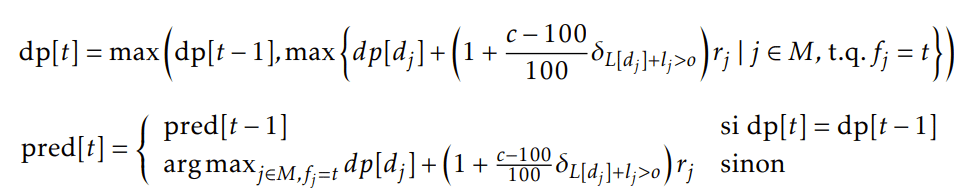
Après l’obsolescence. Il reste maintenant à trouver l’assignement optimal de missions pour le reste du temps [t0, +inf[. Pour cela, il faut prendre en compte le « gain de récompense » c. La k-ème prochaine missions rapportera [min((c/100)k+1, 2)r⌋ points. On note alors K la valeur tel que (c/100)K < 2 et (c/100)K+1 ⩾ 2. Il se trouve que K est généralement pas très grand et prendra au plus la valeur 70. À partir de la K -ème mission, toutes les missions rapportent le double de leur récompense. On fait alors de la programmation dynamique pour trouver le meilleur assignement de missions dpK [t] dans l’intervalle [t, +inf[ sous ce régime. On a alors :
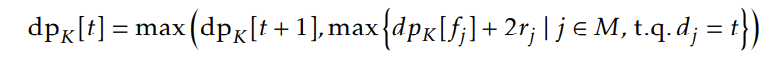
Puis, on fait à nouveau de la programmation dynamique pour trouver dpK −1[t], le meilleur assignement de missions dans l’intervalle [t, +inf[ tel que la première mission rapporte ⌊min((c/100)K , 2)r⌋ points et les missions suivantes 2r points. On a :
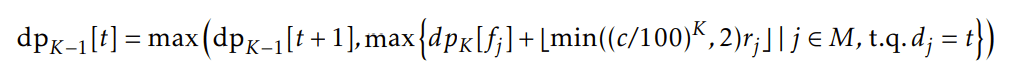
De manière générale, on pose dpk [t] le meilleur assignement de missions dans l’intervalle [t, +inf[ où la première mission de l’assignement correspond à la k-ème mission après t0. On a de la même manière :
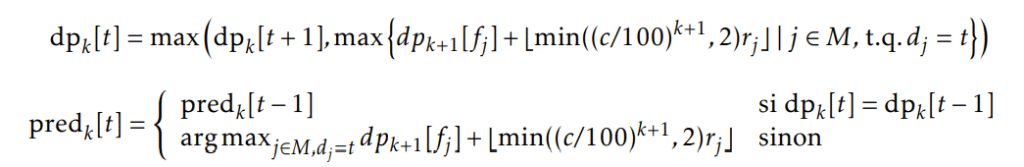
Finalement, l’assignement optimal après obsolescence au temps t0 est donné par (dp1[t0], pred1[t0]). On assigne alors toutes les missions de cette solution optimale au chronobot actuel.
2. c ⩽ 100
Après l’obsolescence Sans doute le cas le plus intéressant car c’est celui qui rapporte le plus de points sur le troisième testcase. L’idée, c’est de calculer le meilleur score qui peut être obtenu dans un intervalle [t, +inf[ après obsolescence du chronobot. Encore de la programmation dynamique ! Cette fois-ci, on a :
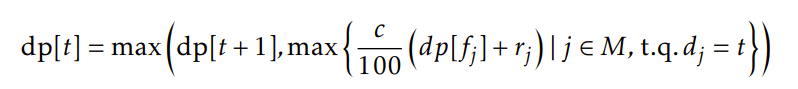
A noter que c’est une approximation car on omet les parties entières. J’arrête également d’écrire la relation pour pred[t] qui découle naturellement de dp[t]. Si on entre en obsolescence en commençant une mission à partir du temps t on connaît alors le meilleur score qui peut être obtenu après obsolescence ainsi que l’assignement Rt de mission qui donne ce score.
Avant l’obsolescence. Il reste désormais à savoir quelles missions sélectionner dans l’intervalle ] − inf, t] avec pour contrainte que la somme des longueurs des missions sélectionnées ne doit pas dépasser o. C’est un problème du sac à dos, mais avec un sac trop gros et trop d’objets pour résoudre le problème de manière exacte. De plus, il y a des contraintes sur les choix d’objets/missions puisque deux missions ne peuvent pas être choisies si elles s’intersectent temporellement. Il faut donc élaborer une heuristique. Une heuristique bien connue du sac à dos est de trier les objets par ordre décroissant de valeur/poids (ou ici de r/l) et de les ajouter si l’ajout ne fait pas dépasser la charge max du sac à dos. On parcourt alors les missions par ordre décroissant de r/l. Supposons que l’on a déjà choisi un ensemble St de missions et qu’on s’intéresse maintenant à la mission (d, f , r, l). Alors on ajoute la mission à St si et seulement si :
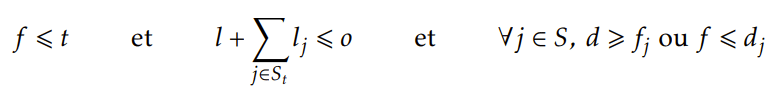

Conclusion. L’assignement final de missions au chronobot actuel est alors St ∪ Rt pour la valeur t qui maximise f (t) + dp[t]. Bien évidement naïvement tout cela a une grande complexité, mais il est possible de ne pas tester toutes les valeurs de t. Voir le code pour une telle implémentation.
3. Ordre d’ajout des chronobots
Au lieu de prendre les chonobots un par un de manière aléatoire, il est possible d’ajouter en priorité le chronobot dont l’ajout augmente le plus le score. Cette stratégie donne de meilleur résultat que l’aléatoire. Secondement, comme cet ordre d’ajout n’est pas optimal, il est encore possible d’amélioration la solution itérativement avec du « local search » en prenant deux chronobots a et b et en les enlevant de toutes missions. On essaye alors d’ajouter a puis b avec les stratégies des précédentes sections et on essaye aussi d’ajouter b puis a et on retient la meilleure solution. Ce local search permet de gagner encore 2/3 millions de points.
Merci pour vos retours d’expérience !
Pendant la durée du concours, des joueurs très sympathiques ont partagé leurs impressions, ce qui a permis d’améliorer la plateforme. Notons par exemple la présentation plus lisible des scores et l’accès à l’ensemble du classement.
Un remerciement particulier à Marie qui a partagé de nombreux mèmes sur sa progression dans le concours !


Super initiative et exercices très intéressants à la difficulté progressive avec un dernier exercice d’optimisation très challengeant. Concours réussi ! Félicitations !
Participant de Code On Time
Les énoncés étaient super bien pensés et intéressants ! Néanmoins, j’aurais voulu avoir 2 weekends pour travailler dessus pour essayer de détrôner Nanored !!!
Participant de Code On Time
Pour aller plus loin

Meritis décroche la 3ème place du CodinGame Winter Challenge 2023
L’équipe Meritis a participé le jeudi 16 mars au dernier CodinGame Winter Challenge 2023 et se hisse à la 3ᵉ place du podium.
Félicitations à nos 17 participants pour leur superbe classement ! Meritis réalise, de nouveau, une très belle performance en devançant ainsi des Groupes de renommée mondiale tels qu’Ubisoft, Amadeus, Dassault Systèmes, Capgemini, Orange ou encore Thales.

Meritis au Master Dev de France 2023
Meritis a participé au Master Dev France 2023 avec une équipe de 5 experts. Nous avons offert la possibilité à 5 étudiants d’y participer. Bravo aux 8 développeurs qui sont allés en finale !




Pas encore de commentaires