En 1984, un statisticien propose une méthode totalement nouvelle pour représenter les réseaux de neurones, les cartes auto-adaptative de Kohonen. Ablaye nous présente cette méthode appliquée à la classification.
1. Contexte
La classification automatique (clustering) est un outil statistique permettant de regrouper des objets similaires en classes.
Elle est utilisée dans plusieurs domaines sous des noms différents :
- Dans la gestion de relation client, on parle de segmentation, utilisée souvent pour identifier les segments de clientèle, c’est-à-dire l’ensemble des clients ayant le même profil en fonction de certaines caractéristiques : l’âge, le sexe, la catégorie socio-professionnelle, etc…
- Connue en biologie sous le nom de taxinomie, elle sert à regrouper les organismes vivants en groupes appelés taxons
- En informatique, elle permet de réaliser des tâches de reconnaissance de forme, etc…
La classification automatique suppose que les données observées ne sont pas labellisées, c’est-à-dire qu’aucune connaissance sur les classes des objets n’est disponible à priori.
Il existe plusieurs approches pour réaliser des tâches de clustering :
- Méthode de partitionnement : consiste à partitionner les données de façon itérative
- Méthode hiérarchique : créer des groupes par agrégations successives
- Méthode probabiliste : trouver le modèle statistique des données
2. Cartes topologiques de Kohonen
Apparues dans les années 60, les méthodes neuronales inspirées du fonctionnement du cerveau humain ont suscité l’intérêt des mathématiciens et notamment des statisticiens. En général, on peut les utiliser pour réaliser deux types d’apprentissage statistique :
- Apprentissage supervisé : classification et régression
- Apprentissage non supervisé : classification automatique
Dans cet article, je vais vous parler des cartes auto-organisatrices Kohonen (Self-Organizing Map, SOM) appelées aussi cartes topologiques de Kohonen. Il s’agit d’une méthode neuronale développée par Teuvo Kohonen en 1982, utilisée pour réaliser des tâches de classification automatique.
Elles sont composées d’éléments simples (ou neurones formels) assemblés en réseaux de neurones. Leur fonctionnement est fortement influencé par la connexion des éléments entre eux. Les cartes topologiques sont souvent utilisées pour analyser des données observées dont on cherche à comprendre la structure.
Principe de la méthode
La méthode proposée par Kohonen consiste à projeter l’espace des données observées (de grande dimension) sur un espace de faible dimension ; en général 1, 2 ou 3D, appelé carte. Cette dernière est formée d’un ensemble de neurones connectés entre eux selon la notion de voisinage.
Chaque neurone possède :
- Des coordonnées fixes sur l’espace de la carte
- Des coordonnées adaptables sur l’espace des données appelées aussi vecteurs référents, responsables d’une zone de cet espace
Cette projection doit respecter la topologie des données. Elle est basée sur des méthodes de quantification vectorielle qui cherchent à partitionner l’ensemble des observations disponibles en groupements similaires par des algorithmes d’apprentissage. Ces groupements sont caractérisés par leurs structures de voisinage qui peuvent être matérialisées à l’aide d’un espace discret appelé « carte topologique ». Cet espace forme un treillis de faible dimension sur lequel les structures de voisinages sont prises en considération par le modèle. Le choix de la topologie dépend de la nature des problèmes. Les figures ci-dessous montrent quelques exemples de topologies tirés du package R kohonen.
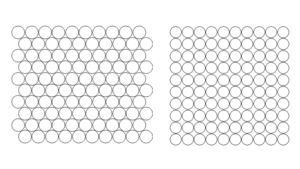
La mise en œuvre d’une carte topologique nécessite une distance δ sur l’espace topologique pour définir la notion de voisinage sur la carte. Il s’agit d’une distance discrète définie par la longueur du chemin le plus court reliant deux neurones sur la carte. Ainsi le voisinage d’ordre d d’un neurone peut être défini comme l’ensemble des neurones situés à une distance d du neurone.
Les distances qui lient les neurones les uns aux autres permettent de varier l’influence relative des différents neurones qui peut être quantifiée par une fonction K. On utilise souvent une famille de fonction KT paramétrée par T appelée parfois fonctions d’activation pour mieux contrôler la taille du voisinage :
Avec :
- T est un terme de paramètre permettant de contrôler l’influence entre neurones
Exemple de fonction de voisinage
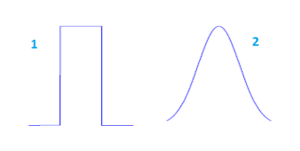
- (1) : Type bubble : il s’agit d’une fonction de voisinage à seuil. Les neurones appartenant au voisinage ont la même influence.
- (2) : Type gaussien : la décroissance de la taille du voisinage s’obtient par diminution de l’écart type qui correspond ici au paramètre T défini ci-dessous. Plus l’écart type est grand, plus l’influence des neurones proches est importante.
3. Algorithme des cartes de Kohonen
Une fois la topologie de carte et les fonctions d’activation choisies, les vecteurs référents sont obtenus par apprentissage à partir des données. Je vais maintenant présenter l’algorithme utilisé pour l’apprentissage de la carte.
- Etape 0 : Initialisation des vecteurs référents W.
- Etape 1 : A chaque itération :
On présente à l’entrée de la carte, un exemple d’apprentissage X(n) choisi
On compare l’exemple à tous les vecteurs référents, le neurone gagnant i est celui dont le vecteur référents Wi(n) est le plus proche de l’entrée X(n) :Où i désigne tour à tour chaque neurone du réseau et Wi son vecteur référent.
- On évalue le voisinage du neurone gagnant
- Mise à jour des poids pour tous les neurones de la carte, l’adaptation est d’autant plus forte que les neurones sont voisins de i* :
– Pour tout i appartenant au voisinage de i*
– α est un paramètre d’apprentissage appelé pas d’apprentissage, qui décroit en fonction de n, et est inférieur à 1.
Cette fonction décroissante α est un élément important car permettant de trouver un compromis entre la vitesse de convergence et la qualité du dépliement de la carte. - Utilisation d’un critère d’arrêt : nombres d’itérations, différence entre les vecteurs poids, erreur de quantification …
Les phases 1, 2 et 3 s’appellent respectivement :
Compétition : Après sélection d’un exemple dans la banque de données, on cherche le neurone qui lui ressemble le plus. Ce neurone dit « neurone gagnant » est souvent noté BMU (Best Matching Unit).
Coopération : Dans cette étape, on détermine le voisinage du neurone gagnant. Il désigne la région de la carte la plus active et qui s’approche le mieux, au sens de la distance utilisée, de l’observation. La taille du voisinage du neurone gagnant est contrôlée par le rayon d’apprentissage.
Adaptation : On modifie le neurone gagnant pour qu’il ressemble plus à l’exemple puis on diffuse l’information sur son voisinage. Cette modification se fait à l’aide de la fonction d’activation qui permet de contrôler l’influence du neurone gagnant sur son voisinage.
La représentation ci-dessous tirée de Wikipédia permet de bien illustrer l’algorithme de Kohonen :
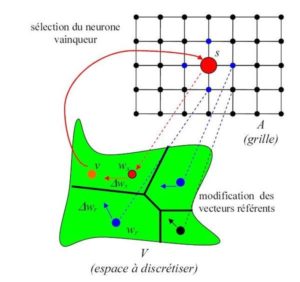
Représentation de l’algorithme d’auto-organisation pour le modèle de Kohonen. Chaque neurone a un vecteur référent qui le représente dans l’espace d’entrée. Un vecteur d’entrée v est présenté. v sélectionne le neurone vainqueur s, le plus proche dans l’espace d’entrée. Le vecteur référent du vainqueur Ws rapproché de v. Les vecteurs référents des autres neurones sont aussi déplacés vers v, mais avec une amplitude moins importante.
4. Classification automatique avec les cartes de kohonen
Une fois une carte apprise, nous disposons des profils types de chaque neurone appelés codebooks. Deux neurones proches dans la carte sont des profils types proches et un ensemble de codebooks contigus représentent un profil particulier dans les données.
Les codebooks constituent un jeu de données sur lequel on peut appliquer une classification hiérarchique ou un k-means pour regrouper les neurones similaires.
La classification d’un nouvel élément peut se faire comme suit :
- Présenter le nouvel élément à l’entrée de la carte
- Identifier le neurone gagnant, celui dont le codebook est le proche du nouvel élément
- Identifier le cluster du neurone gagnant
5. Avantages et inconvénients
Les cartes topologiques de Kohonen présentent de nombreux avantages entre autres :
- C’est une méthode facile à mettre en œuvre, à expliquer
- Une technique de réduction de dimension non linéaire
- Avec ces nombreuses sorties graphiques, les résultats sont faciles à comprendre et à expliquer.
Parmi les limites de cette approche, on peut noter :
- La topologie de la carte est toujours spécifiée à priori
- Elles sont sensibles aux valeurs extrêmes
- Représenter de très nombreuses variables dans un plan bidimensionnel peut s’avérer difficile, tout comme la visualisation et l’interprétation des codebooks
- La convergence vers une solution globale n’est pas assurée
6. Exemple d’application sous R
Pour cette application, je vais générer aléatoirement un jeu de données visant à bien illustrer la classification automatique avec les cartes topologiques de Kohonen.
# generer 3 clusters:
library(MASS)
library(ggplot2)
library(kohonen)
library(dplyr)
# Palette de couleur pour l'affichage des cartes
coolBlueHotRed <- function(n, alpha = 1) {
rainbow(n, end=4/6, alpha=alpha)[n:1]
}
# Le seed permet d'obtenir les mêmes données
set.seed(5678)
Sigma <- matrix(c(10, 3, 3, 2), 2, 2)
a <- mvrnorm(n = 100, c(25, 0), Sigma)
b <- mvrnorm(n = 100, c(10, 5), Sigma)
c <- mvrnorm(n = 100, c(0, 10), Sigma)
data = data.frame(rbind(a, b, c))
data$GROUPE = c(rep("A", 100), rep("B", 100), rep("C", 100))
colnames(data) = c("X", "Y", "GROUPE")
row.names(data) = c(paste0("A", 1:100), paste0("B", 1:100), paste0("C", 1:100))
qplot(x = X, y = Y, color = GROUPE, data = data, geom = "point")
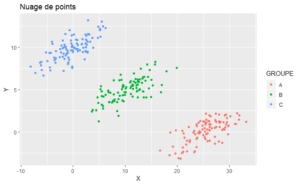
Avant d’appliquer l’algorithme des cartes de Kohonen, il faut s’assurer de la qualité des données. Toutes les données doivent être sous format numérique. Si les données présentent des variables catégorielles, il faudra remplacer chaque modalité d’une variable par une indicatrice (1 si l’individu a la modalité et 0 sinon).
# Normalisation des données
data.scale <- scale(data[,c("X", "Y")], center = T, scale = T)
# Choix du type de carte et de sa taille
som.grid <- somgrid(5, 4, topo="hexagonal", neighbourhood.fct="bubble")
# Apprentissage
som.model <- som(data.scale, grid =som.grid, rlen=1000, alpha=c(0.05,0.01), keep.data = TRUE)
La phase d’apprentissage consiste à trouver les paramètres du modèle optimal :
- Grid : la grille, sa taille, sa forme, le type fonction de voisinage, etc…
- Rlen : le nombre de fois que l’ensemble des données sera présenté au réseau
- Alpha : le pas de l’apprentissage pour contrôler la vitesse d’apprentissage
- Radius : le rayon du voisinage
- Init : les valeurs initiales des vecteurs référents
- …
La librairie kohonen de R présente plusieurs types de visualisation permettant de mesurer de la pertinence de la carte obtenue.
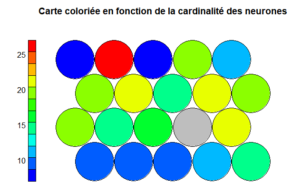
La carte coloriée en fonction de la cardinalité (le nombre d’individus capturés par un neurone) des neurones permet de mesurer la qualité de carte. La distribution de la cardinalité doit être uniforme. Des neurones présentant des cardinalités assez importantes montrent que la taille de carte est petite. De même, la présence de beaucoup de neurones avec des cardinalités nulles suggère que la carte est trop grande.
# Affichage des cartes plot(som.model, type="count", main="Carte coloriée en fonction de la cardinalité des neurones", palette.name=coolBlueHotRed)
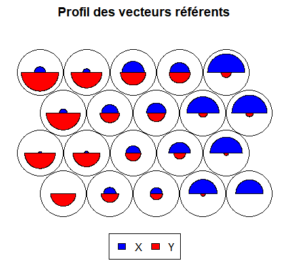
La carte des vecteurs référents permet de visualiser le profil d’individus capturés par les neurones :
# Affichage des vecteurs référents plot(som.model, type="codes", codeRendering="segments", main="Profil des vecteurs référents", palette.name=coolBlueHotRed)
La carte des poids par dimension d’entrée permet de regarder comment chaque zone de la carte réagit par rapport à chaque variable, ce qui sera très utile lorsque l’on interprétera les classes obtenues après classification. Elle permet également d’étudier les corrélations entre les variables au sens de la carte des individus.
# Affichage de larte de poids par dimension d’entrée
par(oma=c(0,0,2,0))
par(mfrow=c(1,2))
df = data.frame(som.model$codes)
for (i in 1:2){
plot(som.model, type="property", property=df[,i],
palette.name = coolBlueHotRed,
main = colnames(df)[i],
cex=0.8)
}
title(main="Carte de poids par dimension d’entrée", outer=TRUE)
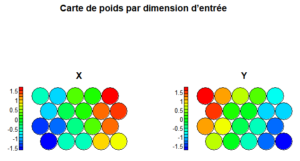
Les variables observées ici ne sont pas corrélées au sens de la carte des individus car les cartes sont totalement différentes et non superposables.
On peut aussi représenter les neurones dans l’espace des données à l’aide des vecteurs référents. Cela permet de voir la qualité de la quantification vectorielle de l’espace d’entrée.
# Ajout des vecteurs référents au nuage de points
df = data.frame(som.model$codes)
df$GROUPE = "CODEBOOK"
dfA = data.frame(data.scale) %>% setNames(nm=c("X", "Y"))
dfA$GROUPE = data$GROUPE
df = rbind(dfA, df)
colours = c('blue', 'green', 'red', 'black')
qplot(x = X, y = Y, color = GROUPE, data = df, geom = "point") + scale_color_manual(values=colours)+ ggtitle("Ajout des vecteurs référents au nuage de points")
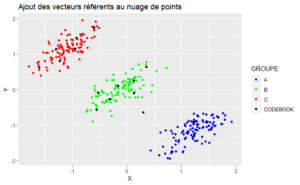
La dernière partie de l’exemple consiste à appliquer la classification automatique des données à partir des cartes de Kohonen. L’idée est de retrouver les trois groupes (A, B et C) qu’on a créés au début du l’exemple.
J’applique l’algorithme des k-means pour regrouper les neurones ayant des profils similaires. Dans un premier temps, j’identifie le nombre de classe optimal avec l’aide de la décroissance de l’inertie intra-classe.
# Choix du nombre de classes
p = 8
df.info <- data.frame(CLUSTER = seq(from = 1, to = p, by = 1))
code.books = data.frame(som.model$codes) %>% setNames(nm=c("X", "Y"))
for (n in 1:p) {
model.kmeans <- kmeans(x = code.books, centers = n, nstart=100)
df.info$WITHINSS[n] <- model.kmeans$tot.withinss
}
ggplot(df.info, aes(CLUSTER, WITHINSS)) + geom_line() + geom_point() + ggtitle("Décroissance de l'inertie intra-classe") +
xlab("Nombre de classe") + ylab("Inertie intra-classe")
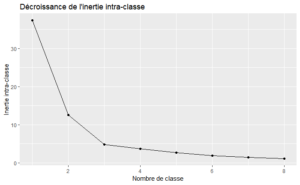
La décroissance de l’inertie intra-classe suggère un nombre de classe égale à 3.
# On fixe le nombre de classes à 3
model.kmeans <- kmeans(x = code.books, centers = 3, nstart=100)
plot(som.model, type="mapping",
bgcol = c("blue", "green","red")[model.kmeans$cluster],
labels = data$GROUPE,
main = "Les clusters sur la carte")
add.cluster.boundaries(som.model, clustering = model.kmeans$cluster)

On retrouve bien les trois groupes définis au début l’exemple. Les neurones fournissent une classification plus fine que les k-means.
Les cartes topologiques de Kohonen constituent un outil puissant de réduction de dimension et de classification automatique. Elles peuvent être vues comme :
- Une extension non linéaire de l’ACP (Analyse en Composantes Principales) dans le cadre d’une réduction de dimension
- Une extension non linéaire de K-means dans le cadre d’une classification automatique
Sources :
Wikipédia – Carte auto adaptative
Vincent Lemaire : Cartes auto-organisatrices pour l’analyse de données
Michel Crucianu, Meziane Yacoub – Cnam : Quantification vectorielle, cartes de Kohonen




Vos commentaires
Merci pour cet article ! Ca m’a rappelé des souvenirs de quand j’avais du dev les SOM en Scala pour ma précédente mission !
Juste, petit question, je n’ai pas compris en quoi « Les neurones fournissent une classification plus fine que les k-means. » ?
Merci !
Merci bien pour tous ces informations monsieur
J ai beaucoup de questions pour vous svp
Je veux appliquer un exemple avec des donnes réelles et appliquer la classification et cartographie de Kohonen sous R .
Merci de avance
Bonjour,
Merci pour l’article.
j’ai besoins de savoir comment visualiser la classification de l’espace d’entrée sur les neurones en sortie avec les couleur seulement, tel que chaque partie de l’espace d’entrée correspond à une couleur, et donc le classement sera visible en affichant pour chaque neurone les espace qu’il lui appartient, et ceci est il possible avec plt.scatter(). Merci
Merci M. Faye, article très intéressant
Peux tu m’envoyer des articles parlant des cartes auto-organisatrices de Kohonen appliquées en imagerie médicale dans un but diagnostique