Cette année encore, j’ai accompagné des équipes d’étudiants au SWERC, une compétition internationale de programmation compétitive dans laquelle on retrouve les meilleurs talents en résolution de problèmes algorithmique. Une belle opportunité de travailler à la résolution d’un problème d’algorithmie. Dans cet article, je vous présente un des exercices et sa méthode de résolution.

Algorithmie : Description du problème

Voici le problème qu’il fallait résoudre :
On nous parle d’un site archéologique à Yinxu, l’ancienne capitale de la dynastie Shang, où l’on a retrouvé des oracles gravés sur des os.
- Chaque oracle peut citer d’autres oracles, mais aucun oracle ne se cite lui-même. On nous garantit qu’il n’existe pas non plus de cycles (c’est-à-dire pas de situation dans laquelle Anne cite Eric, Eric cite Juliette, ni Juliette cite Anne).
- Une divination est dite complète si elle peut prédire la guerre et la paix pour les siècles qui viennent, c’est-à-dire si l’on peut construire une liste d’oracles qui se citent les uns à la suite des autres, sans doublon et en considérant l’ensemble des oracles.
- Un oracle est décrit par un identifiant et la liste des oracles qu’il cite.
On nous demande de déterminer si un ensemble d’oracles constitue une divination complète ou non, pour des ensembles allant jusqu’à 100 000 oracles en 1 seconde.
Algorithmie : Quel raisonnement pour faire émerger une solution
1ere étape d’algorithmie, la modélisation
La première chose à faire est de modéliser le problème, pour le rendre proche d’algorithmes connus. Les oracles qui se citent les uns les autres peuvent être représentés par un graph acyclique orienté :
- Un graph dans lequel on représente chaque oracle par un nœud et les citations par des liens entre les nœuds ;
- Acyclique : il n’y a pas de cycle dans le graph ;
- Orienté : une citation a un sens, c’est-à-dire que « Anne cite Juliette » est différent de « Juliette cite Anne ».
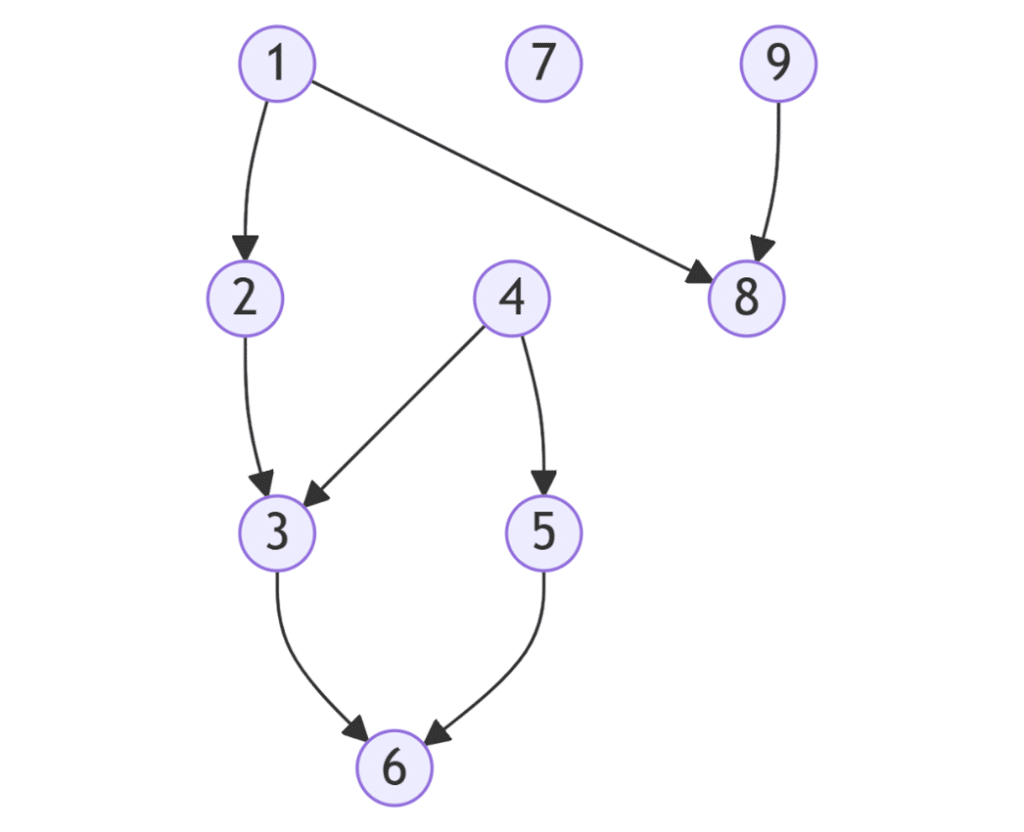
2eme étape d’algorithmie, trouver un algorithme
À présent, on cherche à trouver une façon de construire une chaîne dans notre graph qui contient tous les nœuds. Si on parvient à construire une telle chaîne, alors la divination est complète. Mais si on n’y parvient pas, alors elle est incomplète !
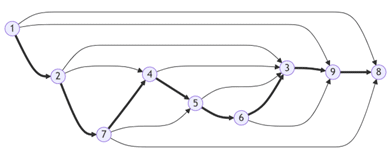
Cette construction est équivalente au fait de construire un ordre topologique sur le graph. C’est un ordre total où l’on peut dire pour toute paire de nœud (a,b) si a <b ou a > b.
La divination est totale si cet ordre existe et s’il est unique.
Découvrez plus en détail la programmation compétitive !
👉 Développement logiciel professionnel vs Programmation compétitive
La question devient : Le tri topologique est-il unique ?
Quelle implémentation pour cet algorithme ?
L’algorithme pour construire ce tri topologique est assez simple :
1- On commence par identifier un nœud qui n’a aucune flèche entrante, ici le « 1 » :
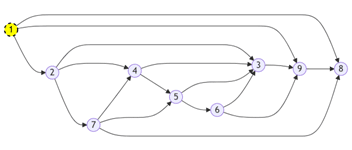
2 / On enlève ensuite ce nœud et l’ensemble de ces flèches sortantes :
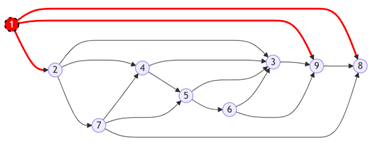
3 / Puis on identifie le nœud suivant :
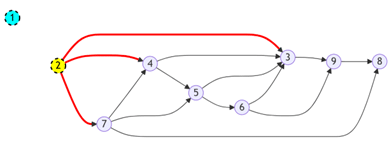
4 / Et ainsi de suite :
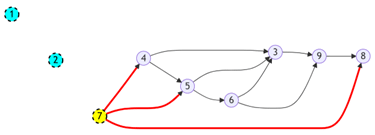
S’il y a plusieurs nœuds sans flèche entrante ou aucun, alors la divination n’est pas totale.
Cet algorithme est une variation de l’algorithme de Kahn qui, lui, construit un des ordres possibles.
Quelles sont les étapes d’implémentation de l’algorithme de Kahn ?
1/ Ajoutez tous les nœuds avec un degré 0 à une file d’attente.
2/ Tant que la file d’attente n’est pas vide :
- Supprimez un nœud de la file d’attente ;
- Pour chaque arête sortante du nœud supprimé, décrémentez le degré d’entrée du nœud de destination de 1 ;
- Si le degré d’entrée d’un nœud de destination devient 0 , ajoutez-le à la file d’attente.
Si la file d’attente est vide et qu’il existe encore des nœuds dans le graphique, le graphique contient un cycle et ne peut pas être trié topologiquement.
3/ Les nœuds de la file d’attente représentent l’ordre topologique du graphique.
À noter : le degré d’un nœud est le nombre d’arrêtes du nœud. En d’autres termes, le degré entrant d’un nœud est le nombre de flèches qui arrivent dans ce nœud.
Et ensuite ?
Pour aller plus loin, ce problème est aussi intéressant dans un contexte parallèle, mais sa mise en œuvre est beaucoup (beaucoup) plus compliqué. Ici, la complexité de notre algorithme (le temps d’exécution en fonction des données) est en temps linéaire de (nombre de nœuds + nombre d’arrêtes).
Cet algorithme est utilisé particulièrement dans des contextes de gestion de dépendances, qu’il s’agisse de tâches, de logiciels, de données, etc. Lors de la compétition, ce problème a été résolu par un peu plus de la moitié des équipes d’étudiants.
Bon code ! Vous pouvez retrouver de tels problèmes d’algorithmique sur https://codeontime.fr, régulièrement des événements y sont organisés pour dev et non dev sur des sujets d’algo, de code et de « no-code ».
Découvrez Code On Time avec cet article présentant les éléments de résolution de l’édition 2024 !
Vous avez aimé cet article ?
Abonnez-vous à notre newsletter pour ne rien rater de l’actualité Tech et Finance.




Pas encore de commentaires