La probabilité risque-neutre est un concept fondamental en mathématiques financières. Il fournit un cadre analytique précieux pour l’évaluation d’instruments financiers complexes tels que les options et les dérivés. La raison : elle repose sur des hypothèses théoriques comme l’absence d’opportunité d’arbitrage ou la complétude des marchés, offrant ainsi une perspective simplifiée pour l’analyse quantitative des marchés financiers. Nous allons dans cet article définir le socle théorique dans lequel s’inscrit cette probabilité, mais également explorer un des modèles financiers qui découle de ce concept et fournir une application pratique.
C’est quoi la probabilité risque-neutre ?

Tout d’abord, rappelons certaines définitions nécessaires à la compréhension du contexte dans lequel s’inscrit la probabilité risque-neutre.
? Découvrez comment les méthodes statistiques et l’essor des big data révolutionnent les marchés financiers grâce à notre article « Introduction aux stratégies d’arbitrage statistique« .
Qu’est-ce que l’absence d’opportunités d’arbitrage ?
En théorie financière, l’arbitrage est une opération qui n’implique aucune mise de fonds, et qui n’engendre que des flux de trésorerie positifs ou nuls (positifs dans certaines éventualités mais en aucun cas négatifs).
Une opportunité d’arbitrage peut se présenter, par exemple, quand il est possible de synthétiser un actif A par une combinaison de deux actifs B et C. Dès lors, si l’on appelle respectivement A, B et C les séquences de flux générées par les actifs A, B et C, il existe deux scalaires λ1 et λ2 tels que :
A = λ1B + λ2C, avec certitude.
Une opportunité d’arbitrage se présenterait alors aujourd’hui si les prix PA, PB et PC respectivement de A, B et C ne satisfaisaient pas la relation de cohérence suivante :
PA = λ1PB + λ2PC
En effet, si PA > λ1PB + λ2PC, alors l’arbitrage consiste à acheter λ1 unités de B et λ2 unités de C et à vendre A, éventuellement à découvert, ce qui engendre aujourd’hui le flux positif f = (PA – (λ1PB + λ2PC)).
Ultérieurement, les flux payés à l’acheteur de l’actif A couvriront exactement les flux reçus du fait de l’achat de B et C. La chronique des flux est ainsi {f, 0, …,0}, ce qui consiste à l’évidence à un « repas gratuit » (free lunch en anglais) pour l’arbitragiste.
La condition d’absence d’opportunité d’arbitrage (notée AOA dans la littérature scientifique et dans la suite de cet article) permet de fonder de nombreux modèles financiers et constitue la pierre angulaire de la théorie financière moderne. Elle est théoriquement justifiée par l’unicité des prix caractérisant un marché en concurrence pure et parfaite.
L’AOA est également liée au maintien de la cohérence des prix des actifs financiers. Si des opportunités d’arbitrage existaient, elles entraîneraient par conséquent des mouvements rapides des prix des actifs pour éliminer ces opportunités, créant ainsi un mécanisme d’ajustement automatique qui rétablit l’équilibre.
C’est quoi un marché complet ?
Un marché complet se réfère à un marché où il existe suffisamment d’instruments financiers disponibles pour permettre la réplication parfaite de n’importe quelle stratégie d’investissement. Ainsi, tout profil de rendement peut être obtenu en combinant judicieusement ces actifs. Cette condition est souvent liée à l’AOA, car la possibilité de répliquer parfaitement toute stratégie limite les opportunités de réaliser des gains sans risque en exploitant les déséquilibres temporaires du marché.
Taux sans risque
Le taux sans risque, également appelé taux d’intérêt sans risque, est le rendement attendu d’un investissement qui est considéré comme totalement exempt de risque financier. Cela signifie que l’investissement est perçu comme sûr, sans risque de défaut de paiement.
En général, le taux sans risque est associé aux obligations d’État émises par des gouvernements considérés comme économiquement stables et fiables. En Europe par exemple, l’obligation allemande est souvent considérée comme un actif sans risque et le rendement de ces obligations à long terme est souvent utilisé comme une approximation du taux sans risque.
Méthode de probabilité risque-neutre
En AOA et dans un marché complet, la valeur d’un actif s’exprime comme une espérance actualisée de son payoff. Cette espérance est calculée sous la probabilité dite « risque-neutre » p et l’actualisation est opérée au taux sans risque r.
Ainsi, sous la probabilité risque-neutre, tous les actifs du marché ont la même espérance de rentabilité, égale au taux sans risque r. Chose importante, cette appellation ne signifie pas que l’investissement n’est pas risqué, mais qu’aucune prime de risque ne majore l’espérance de rentabilité des titres risqués quand l’espérance est calculée sous la probabilité p, d’où l’appellation risque-neutre.
En d’autres termes, la probabilité risque-neutre considère la valeur actuelle d’un actif comme la somme actualisée de ses flux de trésorerie futurs au taux r.
Considérons un actif dont la valeur future est F dans T années. La valeur actuelle P de cet actif, en supposant un taux d’actualisation constant r, est donnée par la formule fondamentale :
P=\frac{F}{(1+r)^T}Appliquons maintenant ces concepts à l’évaluation d’une option d’achat sur une action.
? Plongez dans notre article pour comprendre comment la crise de 2008 a mis en lumière les failles du risque de contrepartie et les actions entreprises pour renforcer la sécurité financière. Une lecture essentielle pour mieux gérer les risques financiers !
A retrouver ici : Le risque de contrepartie : une menace persistante pour la stabilité
Pricing d’option européenne sous la probabilité risque-neutre dans un modèle à une période et deux états du monde
Avant d’entrer plus dans le détail, il est important de rappeler ce qu’est une option.
Rappel sur les options
Une option est un actif pour lequel l’acheteur verse au vendeur une somme d’argent (appelée prime de l’option) en date initiale et reçoit en contrepartie, à une date future, un flux positif ou nul (appelé payoff de l’option) dont le montant dépend de l’évolution d’un actif dit sous-jacent. On dira que l’option est standard si le sous-jacent ne délivre aucun flux de trésorerie (par exemple : dividende, coupon…) avant l’échéance.
Il existe deux catégories d’options :
- L’option d’achat dite call : elle confère le droit et non l’obligation d’acheter un actif sous-jacent au prix d’exercice K (strike price) ;
- Et l’option de vente dite put : elle confère le droit et non l’obligation de vendre un actif sous-jacent au prix d’exercice K. Le strike price K est fixé à la date d’émission de l’option (t = 0).
On dit qu’une option est « européenne » si elle peut être exercée uniquement à la date d’expiration T, appelée date d’exercice, date de maturité ou date d’expiration de l’option.
L’option est dite « américaine » si l’option peut être exercée à tout moment dans l’intervalle (0, T].
Ces options sont alors dites « vanilles », comparé aux options dites « exotiques », plus compliquées à évaluer et dont certaines ont un payoff qui dépend de la trajectoire du prix du sous-jacent entre 0 et T et non de sa seule valeur en T, comme l’option américaine.
Payoff d’une option européenne
Notons St la valeur de l’actif sous-jacent en t (ex : une action). Le détenteur d’un call européen a le droit d’acheter en T à un prix K l’action valant sur le marché ST. Cette option d’achat n’est intéressante que si St > K. Si tel est le cas, sa position vaudra ST – K. Sinon, il abandonnera l’option et sa position sera nulle.
Le détenteur d’un put européen a le droit de vendre en T à un prix K l’action valant sur le marché ST. Cette option de vente n’est intéressante que si St < K. Si tel est le cas, sa position vaudra K − ST. Sinon, il abandonnera l’option et sa position sera nulle.
On peut donc résumer la valeur d’un call européen ou d’un put européen ainsi :
\mathrm{\Psi }_T^C=\max (S_T-K;0)=C(S_T)\ pour un call ;
\mathrm{\Psi }_T^P=\max (K-S_T;0)=P(S_T)pour un put.
Une option étant un jeu à somme nulle entre l’acheteur et le vendeur de l’option, la position (courte) de ce dernier aura une valeur négative ou nulle :
\mathrm{\Psi }_T^P=\max (K-S_T;0)=P(S_T)pour un call ;
\mathrm{\Psi }_T^P=\max (K-S_T;0)=P(S_T)pour un put.
Un modèle d’évaluation à une période et deux états du monde
Considérons deux marchés en AOA et complets :
- Un marché d’un actif risqué : dans notre cas, il s’agit du marché d’une action qui servira de support pour les options ;
- Et un marché de l’actif sans risque. Par exemple : celui du prêt-emprunt.
En t = 0, on note S la valeur observée de l’action. En t = 1, l’action peut prendre deux valeurs : uS si l’action prend de la valeur ; dS si l’action perd de la valeur (u pour “up” et d pour “down”). ⇒ u et d sont donc des rentabilités brutes (1 + Ru) ou (1 + Rd) représentant deux états possibles du monde : haussier ou baissier.
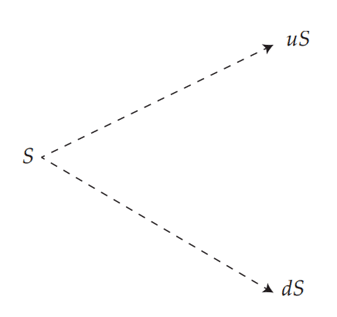
Considérons maintenant les opérations de prêt-emprunt sous la forme d’achat ou de vente d’un actif sans risque qui, pour 1 euro placé en date 0, donne 1 + r euros en date 1.
Remarquons tout d’abord que l’absence d’opportunité d’arbitrage impose la condition suivante :
d < 1 + r < u
En effet, supposons d’abord que d > 1 + r. Le portefeuille composé d’une action, dont l’achat en 0 est financé par un emprunt de montant S, n’exige aucune mise de fonds en date de constitution 0 alors que sa valeur en date 1 est positive dans tous les états du monde :
dS - (1 + r)S > 0
si état d ;
uS - (1 + r)S > 0
si état u.
Un tel portefeuille constitue donc une opportunité d’arbitrage.
Si u < 1 + r : il suffit de vendre l’action et de placer la recette de la vente au taux r pour dégager un profit positif en date 1, ce qui constitue un arbitrage aussi.
Considérons à présent un call sur l’action de prix S, de strike price K et maturité 1.
Si l’état du monde en t = 1 est haussier, le payoff est :
C_1^u=\max (uS-K;0)
Si l’état du monde en t = 1 est baissier, le payoff est :
C_1^d=\max (dS-K;0)
Calcul de la prime de l’option
Pour calculer la prime de l’option, nous allons trouver une stratégie de couverture, appelée aussi portefeuille dupliquant ou synthétisant, qui permette au vendeur de dupliquer le payoff de l’option en date 1, et ainsi d’honorer son contrat.
En date 0, le vendeur de l’option peut investir dans les deux actifs de base, action et actif sans risque. Notons α la quantité d’actions achetées (α >0) ou vendues (α <0) en date 0 et de prix S, et β le montant placé dans l’actif sans risque (β positif indique un prêt, β négatif un emprunt). L’ensemble des portefeuilles admissibles est donc représenté par le couple des deux réels (α, β) et la valeur de constitution en date 0 du portefeuille (α, β) est donnée par :
V_0 = αS + β
En date 1, la valeur de ce portefeuille dépend de l’évolution de l’action et de l’actif sans risque dans un des deux états de notre monde :
V_1^u=αuS+β
si état u ;
V_1^d=αdS+β
si état d ;
On peut maintenant choisir (α, β) de telle façon que la valeur en date 1 du portefeuille soit égale à celle de l’option dans les deux états du monde. Il suffit de résoudre le système de deux équations aux deux inconnues α et β :
\alpha uS+\beta (1+r)=\max (uS-K;0)=C_1^u
\alpha uS+\beta (1+r)=\max (uS-K;0)=C_1^u
dont la solution (α*, β*) est le portefeuille de couverture.
La résolution du système donne :
\alpha*=\frac{C^u_1-C^d_1}{(uS-dS)}\beta*=\frac{C^u_1-\alpha*uS}{(1+r)}L’investissement requis V0 ou valeur constitutive du portefeuille de couverture (α*, β*) est donc :
V_0=\alpha*S+\beta*=\frac{C^u_1-C^d_1}{u-d}+\frac{C^u_1-\frac{C^u_1-C^d_1}{u-d}}{1-r}qui peut se réécrire de la façon suivante :
V_0\ =\frac{1}{1\ +\ r}\left(C_1^u\frac{(1\ +\ r)\ -\ d}{u\ -\ d}+C_1^d\frac{u\ -\ (1\ +\ r)}{u\ -\ d}\right)\ Le portefeuille de couverture ayant, en date 1, une valeur égale à celle de l’option (C1) dans tous les états du monde, en AOA, il doit avoir la même valeur que l’option en date 0 (même raisonnement que plus haut, sinon il suffit d’acheter l’option et de vendre ce portefeuille ou inversement). On a donc : V0 = C0.
Dès lors, on peut affirmer qu’en AOA, la prime de l’option à la date 0 est égale à la valeur V0 de constitution du portefeuille de couverture et écrire :
C_0\ =\frac{1}{1\ +\ r}\left(C_1^u\frac{(1\ +\ r)\ -\ d}{u\ -\ d}+C_1^d\frac{u\ -\ (1\ +\ r)}{u\ -\ d}\right)pour un call ;
P_0\ =\frac{1}{1\ +\ r}\left(P_1^u\frac{(1\ +\ r)\ -\ d}{u\ -\ d}+P_1^d\frac{u\ -\ (1\ +\ r)}{u\ -\ d}\right)pour un put.
On remarquera qu’il n’a pas été nécessaire d’introduire les probabilités statistiques des évènements u et d pour obtenir les prix de l’option : la valeur de la prime ne dépend pas de cette probabilité statistique ou historique d’augmentation du sous-jacent, ce qui peut paraître contre-intuitif. Nous verrons un exemple illustrant cette remarque dans la suite.
Et la probabilité risque-neutre dans tout ça ?
Reprenons l’équation précédente : en cas d’état du monde haussier, le payoff du Call C1u est pondéré par un facteur multiplicatif que nous notons q :
q\ =\ \frac{(1\ +\ r)\ -\ d}{u\ -\ d}En cas d’état du monde baissier, le facteur multiplicatif portant sur est égal à 1 – q :
1-q\ =\ \frac{u\ -\ (1\ +\ r)}{u\ -\ d}Rappelons que l’hypothèse d’AOA implique d < 1 + r < u. Ces deux inégalités impliquent en particulier que q est compris entre 0 et 1 et peut donc s’interpréter comme une probabilité.
On peut donc considérer le couple (q, 1 – q) comme une probabilité portant sur les évènements u et d.
Sous cette probabilité, l’espérance du payoff du call et du put s’écrivent respectivement :
E^q[C_1]=qC^u_1+(1-q)C^d_1
E^q[P_1]=qP^u_1+(1-q)P^d_1
En injectant ces espérances calculées sous la probabilité q dans les formules des primes de l’option, on peut alors formuler la proposition suivante :
« La valeur d’une option s’exprime comme une espérance actualisée de son payoff : cette espérance est calculée sous la probabilité dite “risque-neutre” (q, 1 – q) et l’actualisation se fait au taux sans risque r et on a :
C_0=\frac{1}{1+r}E^q[C_1]et
P_0=\frac{1}{1+r}E^q[P_1]Sous la probabilité risque-neutre, tous les actifs du marché (action, option, actif sans risque) ont la même espérance de rentabilité, égale au taux sans risque r. »
Cette proposition donne une explication de l’appellation risque-neutre donnée à la probabilité : aucune prime de risque ne majore l’espérance de rentabilité des titres risqués quand l’espérance est calculée sous la probabilité q, d’où l’appellation risque-neutre.
Un cas pratique
Soit un parapluie dont la valeur est S = 100 € aujourd’hui en date 0. Demain (en date 1), le prix du parapluie augmentera de 10 % s’il pleut (état u) et diminuera de 10 % s’il ne pleut pas (état d) : uS = 110 et dS = 90.
Supposons par ailleurs que le taux de prêt-emprunt soit nul (les comptes courants ne sont pas rémunérés). On sait par ailleurs que la météo estime qu’il va pleuvoir avec une probabilité p = 90%.
Évaluons la prime d’un call sur le parapluie, de prix d’exercice 100 € et de maturité 1.
Considérons le portefeuille de couverture (α*, β*) comme défini plus haut, par application des formules précédentes. On obtient :
\alpha*=\frac{C^u_1-C^d_1}{uS-dS}=\frac{10-0}{110-90}=0,5\beta*=\frac{C^u_1-\alpha*uS}{1+r}=\frac{10-0,5*110}{1+0}=-45Le vendeur de l’option peut donc dupliquer le flux de l’option par l’acquisition de 0,5 parapluie et l’emprunt de 45 €. On a donc C0 = V0 = α * S + β* = 0,5 x 100 – 45 = 5 €.
La perception de 5 € permet au vendeur de l’option de se porter acheteur du portefeuille (α*, β*).
Cet exemple permet de réitérer le fait que la prime ne dépend pas de la probabilité d’occurrence de l’événement « il pleut » puisque la probabilité p = 90 % introduite dans l’énoncé n’a pas servi.
On pourrait être tenté d’évaluer la prime de l’option à l’aide d’un calcul d’espérance faisant intervenir des probabilités statistiques : dans le cas où il pleut, le vendeur se voit dans l’obligation de payer 10 €. La probabilité de cet événement est de 90 %.
Dans le cas contraire, il ne doit rien payer. La moyenne de son décaissement est donc égale à 0,9 x 10 € = 9 €. Un tel raisonnement aboutit donc à une surévaluation de la prime du call qui, comme on l’a démontré, ne vaut que 5 €.
Calculons maintenant le rendement de l’actif risqué sous la probabilité risque-neutre q. En absence de dividende, l’espérance de son taux de rentabilité se confond avec l’espérance de son taux de croissance. De plus, les paramètres u et d s’interprètent comme des rentabilités brutes (1+ taux de rentabilité) dans deux conjonctures, respectivement haussière et baissière. Le taux de rentabilité peut donc prendre deux valeurs u – 1 et d – 1. On a donc :
q\ =\ \frac{(1\ +\ r)\ -\ d}{u\ -\ d}=\frac{1\ -\ 0,9}{1,1\ -\ 0,9}=0,5E^q[\frac{S_1-S_0}{S_0}]=q(u-1)+(1-q)(d-1)=0,5*10\%-0,5*10\%=r=0On retrouve ici le résultat énoncé plus haut : la rentabilité moyenne sous q est égale au taux sans risque r = 0 % (le taux de prêt-emprunt nul car les comptes courants ne sont pas rémunérés).
Le même calcul, mené sous la probabilité statistique p = 90 % donne :
E^q[\frac{S_1-S_0}{S_0}]=p(u-1)+(1-p)(d-1)=0,9*10\%-0,1*10\%=8\%Notons que la rentabilité moyenne calculée sous p est strictement supérieure à r. L’écart est appelé excès de rentabilité et s’interprète comme une rémunération du risque de l’action ou prime de risque.
Les limites du modèle
Bien que l’absence d’opportunités d’arbitrage et la complétude des marchés renforcent la robustesse des modèles financiers, il est important de noter que dans la réalité, des opportunités d’arbitrage peuvent parfois émerger temporairement et des limitations telles que les coûts de transaction, les contraintes réglementaires et les informations imparfaites peuvent entraver la possibilité de créer une réplication parfaite de toutes les stratégies.
Conclusion
En conclusion, la probabilité risque-neutre demeure un outil mathématique essentiel en finance, offrant une approche systématique pour évaluer des instruments complexes tels que les options puisque, sous cette probabilité, tous les actifs du marché ont la même espérance de rentabilité, égale au taux sans risque r.
On retiendra que la probabilité risque-neutre est une probabilité construite mathématiquement hors d’un cadre statistique. Et par conséquent qu’elle s’écarte donc de la notion de probabilité réelle ou historique, et que de nombreux facteurs réalistes limitent cette approche théorique.
Ressources
- Finance de marché, instruments de base, produits dérivés, portefeuille et risques – R. Portrait, P. Poncet (2014)
- Méthodes et instruments de la finance – G. de Truchis, E. Dumitrescu
- Absence d’opportunité d’arbitrage et probabilité risque-neutre – F. Planchet (2023)

Vous avez aimé cet article ?
Abonnez-vous à notre newsletter pour ne rien rater de l’actualité Tech et Finance.



Pas encore de commentaires