FRTB : VaR vs ES

Dans le cadre de FRTB, l’exigence met l’accent sur la différenciation des banking books et des trading books afin d’éviter les arbitrages réglementaires. Il est également nécessaire de définir les instruments pris en compte dans le calcul des risques et d’identifier plus précisément les corrélations entre les portefeuilles.

En parallèle, l’Expected Shortfall (ES) est introduit en tant que nouvelle mesure du risque pour permettre de prendre en considération les cas extrêmes des queues de distribution. Ce qui pourrait être plus pertinent pendant les périodes de crises ou lors d’événements extrêmes.

De plus, l’horizon de liquidité doit être précisé afin de distinguer les impacts de tous les produits dans le calcul du risque selon le niveau de liquidité.

Que va alors induire la mise en place de cette réglementation ? Une hausse des exigences des fonds propres liée aux activités de marché pour les communautés financières, notamment les banques. Ces dernières devront donc revoir la totalité du calcul des risques réglementaires, ce qui impliquera de lancer de nombreux projets pour mettre à jour les outils de calcul et de reporting. Avec pour principaux impacts : une augmentation des besoins en gestion et des capacités d’analyse des données, associée à la nécessité d’assurer la qualité des données utilisées pour les calculs.

Le passage de la VaR à l’ES

Un point essentiel de FRTB consiste donc à remplacer la VaR (vous allez trouver le détail sur la VAR ici) par l’ES comme mesure du risque. Les grands volumes de données historiques et les capacités de traitement des données sont primordiaux pour répondre à l’objectif d’implémenter l’ES, ce dernier étant ultra-sensible aux données non-normalisées (je vous invite à découvrir le détail sur l’ES ici).

Exigé par les régulateurs, chaque banque doit alors calculer l’ES dans son ensemble ainsi qu’au niveau de chaque desk de trading. De plus, les banques doivent effectuer des calculs quotidiens d’attribution de performances et de backtesting, qui nécessitent une grande puissance de calcul.

Depuis son introduction dans les années 90, la VaR est considérée comme une mesure de risque standard et simple entre les banques. Elle combine la dimension quantitative et probabiliste qui mesure la perte potentielle maximale qu’un portefeuille est prêt à subir sur un horizon de temps donné, avec une probabilité donnée (un intervalle de confiance).

Grâce à sa simplicité, la VaR, en tant que seul indicateur synthétique, donne une évaluation du risque d’un portefeuille quelle que soit sa composition. Cette seule mesure facilite les comparaisons entre les différents portefeuilles, et permet aux banques de communiquer auprès des régulateurs de manière compréhensible.

En revanche, la VaR possède des limites incontournables :

• Est-il pertinent de prévoir l’avenir par les données historiques (VaR historique) ?
• Les hypothèses de calcul de la VaR sont-elles correctes (VaR paramétrique avec une hypothèse de distribution) ?

Pour les distributions non normales, le calcul de l’Expected Shortfall prend en compte ce que la VaR ne fait pas, à savoir la perte potentielle sur un marché soumis à un stress particulier comme les événements extrêmes, les corrélations, etc.

Après la crise financière de 2008, l’Expected Shortfall est de plus en plus utilisé par les communautés financières. Dans la recommandation du Comité de Bâle, la FRTB impose aux banques de mettre en œuvre et d’utiliser l’ES pour compléter la VaR, et la remplacer un peu plus tard.

Tout simplement, l’ES est défini comme la perte moyenne quand on se trouve dans les q% de la queue de la distribution des rendements (le pire q%). Cela signifie que l’ES est plus sensible à la forme de la distribution des rendements au-delà du seuil de q%.

Les avantages de l’ES par rapport la VaR

• Mesure supérieure du risque de queue (tail risk) : l’Expected Shortfall (ES) prend en compte les queues épaisses dans les distributions des rendements. Les transactions à valeur relative (long / short strategy) présentent souvent des queues épaisses, donc l’ES est mieux adaptée pour quantifier le risque extrême, essentiellement dans le cas avec un grand kurtosis.

Par exemple : la stratégie « short volatility » possède souvent un Ratio de Sharpe élevé. Toutefois, le risque de queue n’est pas pris en compte dans le Ratio de Sharpe. Une meilleure mesure serait de remplacer le Ratio de Sharpe par le rendement total divisé par l’ES.

• Concentration sur la couverture du risque extrême : l’ES permet aux investisseurs de réviser leurs hypothèses de calcul et d’identifier clairement le risque de queue et le couvrir plus efficacement, afin d’améliorer les stratégies de couverture de la queue des distributions des rendements.
• Mesure du risque d’événement : la VaR n’est pas adaptée pour capturer le risque lié à un événement car les distributions des rendements historiques n’incluent pas les déclenchements des évènements.

Par exemple : les impacts des prix liés aux nouvelles des entreprises (news flow), les arbitrages des fusions-acquisitions, etc. L’ES en tant qu’une moyenne prend en compte ce risque d’événement.

• Traitement alternatif de la corrélation : la corrélation est importante pour quantifier les avantages en termes de réduction des risques ou de diversification. Le calcul de l’ES intègre des changements de corrélation potentiellement importants car il s’agit d’un calcul impliquant la queue exactement là où la corrélation change, contrairement aux calculs de VaR traditionnels.

Par exemple, dans le cadre de d’un « Basis Trade » (future vs spot), la stabilité des corrélations sur les marchés normaux conduit à une VaR faible alors que le portefeuille pourrait avoir une perte potentielle importante si les corrélations changeaient de manière significative. L’ES apparaît ainsi mieux adapté pour mesurer ces changements de corrélations.

• Mesure de risque directement lié aux liquidités : dans les transactions des produits dérivés, la VaR stressée entraîne une probabilité importante que le fond ne sera pas en mesure de répondre aux appels de marge. L’ES permet d’utiliser un horizon suffisamment long pour intégrer la liquidité des actifs et les changements des conditions du marché pendant le stress afin d’avoir du temps pour repositionner le portefeuille.
• Calcul de la hauteur des pertes : la VaR ne décrit pas la hauteur de la perte au-delà de la perte maximale. L’ES propose une moyenne des pertes afin de donner une mesure quantitative dans les q% pire cas.
• Propriété Sous-Additive : la VaR n’est pas sous-additive. En revanche, les banques peuvent utiliser la propriété sous-additive de l’ES pour consolider les différents portefeuilles afin de réduire les exigences des fonds propres associés.

Une comparaison entre l’ES et la VaR

Rappel : pour un portefeuille et un horizon de temps :

• VaR : la perte potentielle maximale avec une probabilité donnée (q%)
• ES : la moyenne des pertes qui n’apparaît que dans les q% pires cas

Portefeuille réplique la performance de S&P

Horizon du temps : 1er juillet 2018 – 1er juillet 2019, soit 250 observations

Calculer la performance de chaque jour avec le prix de clôture : 249 performances

Calculer la moyenne des performances : 0,04 %

Calculer l’écart type des performances : 0,97 %

VaR avec la méthode paramétrique (l’hypothèse de la distribution normale) :

• 99 % de l’intervalle de confiance : 1 % de queue à gauche dans la distribution des rendements : -0,022267152
• 95 % de l’intervalle de confiance : 5 % de queue à gauche dans la distribution des rendements : -0,015640958

VaR avec la méthode historique :

• 99 % de l’intervalle de confiance : 1% de queue à gauche dans la distribution des rendements : -0,031629673
• 95 % de l’intervalle de confiance : 5% de queue à gauche dans la distribution des rendements : -0,019036216

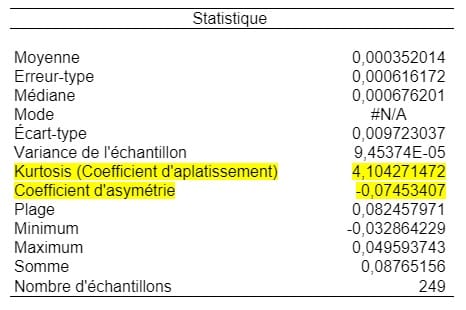
La Kurtosis est une notion importante de classification et d’analyse des distributions de probabilités. Pour une distribution normale, la Kurtosis doit être égal à 3. Dans notre cas, la Kurstosis est de +4,1, ce qui explique les queues épaisses.

Le coefficient d’asymétrie (skewness) est une mesure de l’asymétrie de la distribution des rendements. Pour une distribution normale, cette valeur doit être égale à 0. Dans notre cas, le coefficient d’asymétrie est de - 0,07, ce qui signifie que notre distribution a légèrement dérivé par rapport à la distribution normale. Il y a plus de valeurs dans la queue à gauche, ce qui explique la différence entre les VaR paramétriques et les VaR historiques calculées.

99 % de l’intervalle de confiance :

• VaR Paramétrique : -0,022267152 & VaR Historique : -0,031629673

95% de l’intervalle de confiance :

• VaR Paramétrique : -0,015640958 & VaR Historique : -0,019036216

Graphiquement, la distribution n’est pas normale comment suit :

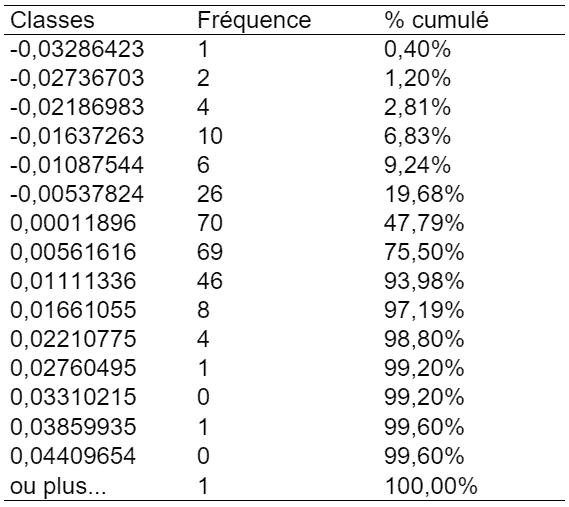
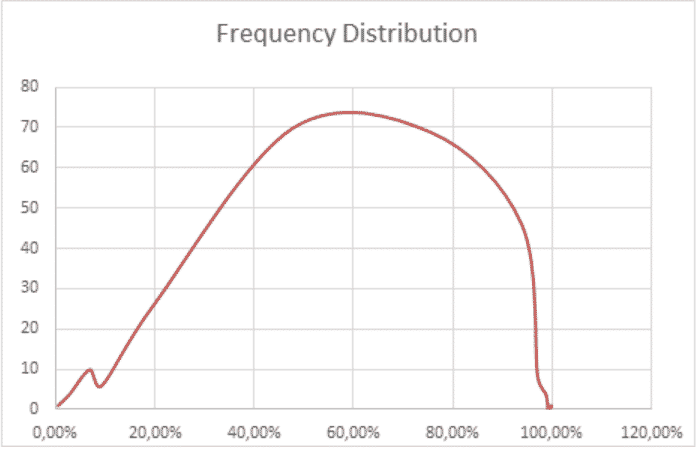
Expected Shortfall :

• 99 % de l’intervalle de confiance : la moyenne des pertes qui n’apparaît que dans 1% des pires cas : -0,032031189.
• 95 % de l’intervalle de confiance : la moyenne des pertes qui n’apparaît que dans 5 % des pires cas : -0,02423928.

Il est évident que l’ES est toujours supérieur à la VaR.

Que conclure de cette comparaison ?

table {
border-collapse: collapse;
}
th, td {
border: 1px solid black;
padding: 10px;
text-align: left;
}

	Intervalle de confiance 99%	Intervalle de confiance 95%
VaR (Value at Risk)	VaR Paramétrique : -0,022267152 VaR Historique : -0,031629673	VaR Paramétrique : -0,015640958 VaR Historique : -0,019036216
ES(Expected Shortfall)	-0,032031189	-0,02423928

Application de l’ES et la VaR dans un portefeuille personnalisé

Ce portefeuille est composé par trois classes d’actifs : soit 60 % d’actions, 30 % d’obligations et 10 % de commodités. Le détail de la composition est comme suit :

Classe d’actif	Produit sélectionné	Allocation d’actif
Action :	Russell 2000 Index Fund	60%
Obligation :	iBoxx High Yield Corporate Bond	30%
Matière première (Métaux précieux) :	Dow Jones Precious Metals Index	10%

La valeur nominale du portefeuille est d’1 million d’euros.

Horizon du temps : 1er décembre 2018 – 31 janvier 2019, soit 38 observations.

Classe d’actif	Performance	Écart type
Action :	-0,08 %	1,67 %
Obligation :	0,05 %	0,58 %
Matière première (Métaux précieux) :	0,35 %	1,93 %

La FRTB exige le calcul de l’ES avec 97,5 % de l’intervalle de confiance.
L’ES de ce portefeuille calculé est : – 0,025927432.