Vous saurez tout sur la VaR

Le concept de VAR (Value at Risk) a été introduit dans les années 80 dans le domaine des assurances. Depuis, il a été popularisé par la banque JP Morgan au cours des années 90, adopté par la réglementation bancaire Bâle II puis adopté par Solvency II pour les assurances. Il s’agit d’une mesure facilement compréhensible applicable à beaucoup de situations et qui permet de quantifier le risque. La VAR indique le maximum de perte potentielle, pour un intervalle de confiance et une période de temps donnée.

On parlera par exemple d’une VaR de 1.5% sur un portefeuille de 100 millions d’euros avec un intervalle de confiance de 5% et un horizon temporel d’une semaine.

Cela signifie que le portefeuille a 5 % de chance de connaître une perte supérieure à 1.5% de sa valeur (soit 1.5 million d’euros) d’ici une semaine. Une autre façon de voir les choses consiste à dire que d’ici une semaine il y a 95 % de chance que la perte réalisée sur le portefeuille soit inférieure à 1.5 million d’euros.

L’horizon temporel sélectionné dépend du type de portefeuilles sur lequel porte le calcul. Pour un portefeuille actions ou obligations, une VaR mensuelle ou trimestrielle sera adaptée. Une VaR journalière ou hebdomadaire sera plus appropriée pour un portefeuille contenant des produits dérivés ou à fort effet de levier.

De même, l’intervalle de confiance choisi (1%, 5%) affectera significativement le montant de la VaR. Dans un second temps, il sera aussi intéressant d’étudier la partie située au-delà de la VaR indiquée, c’est-à-dire la zone des pertes extrêmes située à gauche de la queue de distribution (zone orangée sur le graphique ci-dessous en faisant l’hypothèse de normalité sur la distribution des PnL quotidiens).

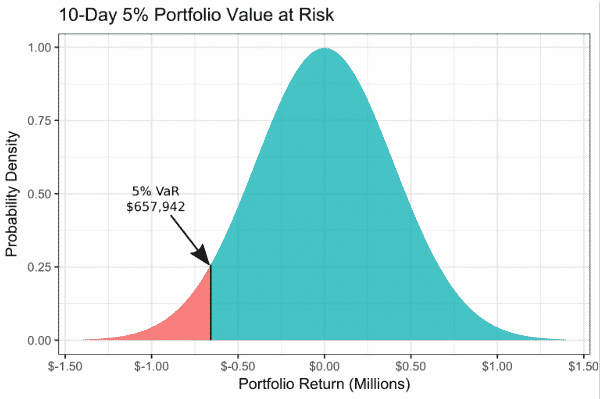
Pour déterminer la VaR d’un portefeuille, nous distinguons 3 méthodes différentes que nous détaillerons en mettant en perspective les avantages et inconvénients de chacune d’entre elles.

Ces 3 méthodes de VaR sont les suivantes : VaR historique, VaR paramétrique et VaR Monte Carlo.

La plus simple à calculer et interpréter : la VaR historique

La VaR historique consiste à récupérer l’historique des prix des actifs composant mon portefeuille de façon à calculer l’évolution de sa valeur au fil du temps. Les prix varient quotidiennement alors que les positions de chaque actif composant mon portefeuille sont figées en fonction du poids de chaque actif aujourd’hui.

Ainsi, nous sommes en mesure de déterminer alors les PnL (Profits & Losses) quotidiens de mon portefeuille que l’on classe ensuite par ordre décroissant. En fonction du nombre de PnL ainsi calculés et de l’intervalle de confiance désiré, la VaR historique correspondra à la valeur du PnL correspondante.

Exemple

On reconstitue 4 ans d’observation quotidienne (à raison de 250 observations annuelles), on aura donc obtenu et classé 1 000 PnL. Si l’intervalle de confiance retenu pour le calcul de VaR est de 5%, ma VaR historique correspondra au 50ème plus faible PnL (5% * 1000 = 50).

Exemple de calcul de VaR historique avec 100 PnL

100 rendements quotidiens ont été collectés sur un portefeuille de 100 millions d’euros. Après les avoir classés par ordre décroissant, voici les 5 plus petits rendements journaliers :

-0.0101 ; -0.0097 ; -0.0043 ; -0.0038 ; -0.0018

La VaR à 5% correspondra à la 5ème plus petite observation soit -0.18%.

Ainsi on pourra conclure que le portefeuille à 5% de chances de réaliser une perte supérieure à 180 000 euros sur une journée (0.0018* 100 000 000 = 180 0000).

La principale force de la VAR historique réside sur les 2 points suivants :

• Facilité de calcul et d’interprétation
• Ne présuppose pas une forme de distribution particulière des rendements des actifs

La VaR historique suppose toutefois que les mouvements de prix ayant affecté mon portefeuille dans le passé sont amenés à se reproduire. Elle ignore donc le profil particulier de certains actifs dont les distributions changent au cours du temps. De plus, certains gérants réalisent un fort turnover au sein de leur portefeuille : dans ce cas la VAR doit être actualisée régulièrement pour refléter le changement de composition du portefeuille. Par ailleurs, il est difficile de récupérer un historique de prix sur certains produits, notamment les options.

La VaR paramétrique : suppose une distribution normale des rendements

La VaR paramétrique repose sur l’hypothèse que les rendements des actifs suivent une loi normale. C’est globalement vrai pour un portefeuille contenant des actions voire même des obligations mais cette proposition est largement remise en cause dès lors que le portefeuille comprend des produits dérivés (options, futures, etc.) pour lesquels le profil de distribution des rendements est très asymétrique.

Pour calculer la VaR paramétrique sur un portefeuille, il faut tout d’abord construire ce que l’on appelle une matrice de variance-covariance. Il s’agit d’un tableau constitué de la variance de chaque actif (un indicateur mesurant la volatilité de chaque actif c’est-à-dire la dispersion de ses performances autour de son rendement moyen) et la covariance entre chaque paire d’actifs (degré de corrélation existant entre deux actifs).

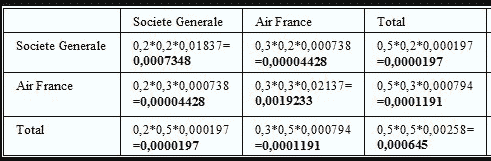
En effet, en finance, pour apprécier le risque d’un portefeuille, on a besoin de deux dimensions : la volatilité de chaque actif d’une part, c’est-à-dire la façon dont le prix d’un actif aura tendance à s’écarter de sa valeur moyenne et d’autre part, la corrélation qu’il existe entre chaque actif, c’est-à-dire l’intensité du lien existant entre deux actifs. Plus un actif est corrélé avec un autre, plus ils auront tendance à évoluer dans le même sens, plus la corrélation de ces 2 actifs sera proche de 1.

Plus les actifs composant un portefeuille sont volatiles et plus les actifs sont corrélés entre eux (c’est-à-dire plus ils auront tendance à varier dans le même sens et avec la même intensité), plus le portefeuille sera risqué. Pour réduire le risque d’un portefeuille, il existe deux solutions : celle consistant à limiter le poids des actifs risqués (ou augmenter celui des actifs peu risqués), ou celle consistant à favoriser l’effet de diversification au sein du portefeuille (sélectionner des actifs peu corrélés ou décorrélés entre eux).

Une fois cette matrice de variance-covariance constituée et connaissant la pondération de chaque actif au sein de mon portefeuille, on est capable de déterminer le rendement moyen et la volatilité (donnée par l’écart-type, c’est-à-dire la racine carrée de la variance) de mon portefeuille. En supposant que chaque actif le composant a un profil de rendement normalement distribué, on pourra déterminer la VaR en appliquant les coefficients de loi normale. Signalons d’ailleurs que les rendements moyens des actifs et leur volatilité sont calculés à partir d’un historique de prix.

Exemple

Calcul VaR paramétrique sur un portefeuille de 100 millions d’euros et un intervalle de confiance de 5%

Supposons que le rendement moyen de ce portefeuille soit de 8% annuel et que son écart-type annuel (indicateur de volatilité) soit de 14%. Quelle est la VaR annuelle pour un intervalle de confiance de 5% ?

Selon la loi normale, le nombre d’écart-type associé à un intervalle de confiance de 5% est de 1.65, c’est-à-dire qu’il y a 5 % de chance pour que le portefeuille dévie de plus de 1.65 fois l’écart type depuis son rendement moyen.

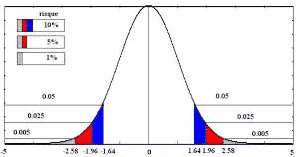En appliquant la formule suivante, nous pouvons aisément calculer la VaR du portefeuille

= [8 % -1.65(14%)] *100 000 000

= -15.1% * 100 000 000

= -15 100 000 €

Où :

• correspond au rendement espéré du portefeuille,
• la valeur du portefeuille
• est le nombre de déviations en termes d’écart-type depuis la valeur moyenne (dépend de l’intervalle de confiance choisi)
• est l’écart type du portefeuille

On peut donc conclure qu’il y a 5% de chance pour que la perte annuelle du portefeuille dépasse 15.1 millions d’euros.

L’intérêt de la VaR paramétrique réside dans la facilité de calcul et la prise en compte de la corrélation des actifs composant le portefeuille. Elle ne s’applique pas en revanche aux portefeuilles contenant des produits optionnels dont la distribution des rendements ne suit pas une loi normale (beaucoup de petites pertes et gros gains peu fréquents). Certains actifs ont au contraire des queues de distribution épaisses (beaucoup plus que celles supposées par la loi normale) ainsi la VAR calculée sous-estimera l’occurrence des phénomènes extrêmes. En effet, la probabilité de réaliser une perte au-delà de 3 écarts types arrive une fois tous les 2 000 ans selon la loi normale, en réalité les crises récentes ont montré que cela se produit une fois tous les 10 ans !

Sur les portefeuilles contenant un très grand nombre d’actifs, la matrice de variance-covariance peut s’avérer extrêmement volumineuse et complexe à calculer.

La VaR Monte-Carlo : la plus précise mais la plus complexe

La VaR Monte Carlo requiert l’utilisation d’ordinateurs performants de façon à générer un très grand nombre de simulations. Pour schématiser, la VaR Monte Carlo mélange à la fois les méthodes de calcul de la VaR paramétrique et de la VaR historique. En effet, les rendements des actifs sont simulés un très grand nombre de fois suivant certaines lois de distribution (pas forcément la loi normale comme pour la VaR paramétrique mais aussi des lois de distribution davantage adaptées aux profils de rendements atypiques).

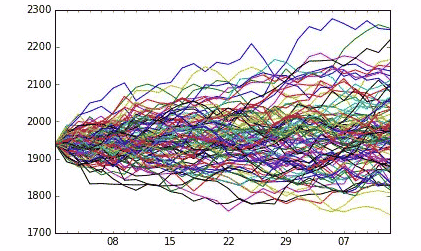
Ensuite, les centaines ou milliers de résultats différents sont classés du plus petit au plus grand comme pour la VaR historique. En fonction du degré de probabilité choisi, le résultat de VaR est alors directement lu à partir de la position du PnL correspondant (50 -ème plus petit PnL pour 1 000 simulations et un intervalle de confiance à 5%).

Le principal avantage de la VaR Monte Carlo réside dans la possibilité d’intégrer un très grand nombre de modèles différents en fonction des actifs composant le portefeuille. Cela permet donc une plus grande précision et une meilleure fiabilité de calcul. C’est aussi son principal inconvénient : les calculs plus complexes et plus gourmands en termes de logiciels sophistiqués renchérissent le coût de sa mise en place. De plus, cela peut déboucher sur un excès de confiance dans les calculs : les calculs seront fiables tant que les modèles sous-jacents utilisés seront robustes et pertinents.

Conclusion

La VaR est désormais devenue un standard dans la gestion des risques en finances, elle est parfois même parfois imposée par les autorités de régulation. De plus, elle permet d’agréger tous les risques en un seul indicateur facilement interprétable.

Toutefois, il ne faut pas écarter ses nombreuses limites : sa mise en place, comme la VaR Monte Carlo, peut s’avérer très coûteuse. La VaR a tendance à se focaliser sur les pertes et ignorer les perspectives de gain. Par ailleurs, la VaR a tendance à sous-estimer l’apparition d’événements extrêmes. Chaque méthode donnera un résultat différent et ce résultat sera d’autant plus fiable que les modèles qui le sous-tendent le sont.

Aussi utile que la VaR puisse être, l’estimation des risques doit être complété par d’autres nouveaux indicateurs tels que l’expected shortfall (ou CVaR pour VaR conditionelle) qui va se focaliser sur la moyenne des pertes situées dans la queue de distribution au-delà de la VaR. L’IVAR (pour Incremental VaR) est aussi un indicateur qui permet de compléter la VaR car il permet d’évaluer l’impact en termes de VaR de l’ajout d’un élément au sein du portefeuille. Enfin, les stress tests permettent de compléter la VaR car ils évaluent l’impact de certains scénarios extrêmes (ayant existé ou simulés) sur les portefeuilles. Ils permettent une grande flexibilité (modification des prix des actifs, des volatilités, des taux, des devises, etc.) et permet de capter certaines conséquences que la VaR est incapable de faire.