Développement logiciel professionnel vs Programmation compétitive

La programmation compétitive est une discipline que j’apprécie particulièrement. J’entraîne ainsi de temps en temps l’équipe de Meritis sur des compétitions ou des entraînements. C’est un sport intellectuel : les participants s’y affrontent en codant des algorithmes avec leur langage de prédilection dans un temps limité. À quoi ressemble alors un tel problème, comment écrit-on l’algorithme qui le résout ? Quelles sont les compétences que l’on utilise ? Sont-elles utiles dans le monde professionnel ?

Il y a quelques idées préconçues autour de la programmation compétitive. Ce n’est pourtant pas du « par-cœur », ce n’est pas que de la vitesse de clavier, ce n’est pas solitaire, et ce n’est pas non plus inaccessible ! Une compétition de code, c’est un ensemble de problèmes à résoudre dans un temps limité.

Comment se passe une compétition de code ?

Les durées peuvent s’étendre de quelques heures à quelques jours. Suivant les cas, les problèmes à résoudre sont évalués sur des cas de test « cachés » ou sur des jeux de données ouverts. Notre algorithme doit alors suivre correctement la consigne ou parfois, sur des cas plus originaux comme Codingame, il « affronte » ceux de nos adversaires dans des simulations de jeux.

Dans tous les cas, pour résoudre le problème, notre algorithme doit avoir la bonne complexité pour répondre en un temps raisonnable, et avec une utilisation acceptable des ressources en mémoire et en CPU. La compétition encourage des compétences en développement rapide de code correct et efficace. Ce ne sont pas les qualités requises pour un développeur professionnel, en tout cas pas seulement. Le code produit en entreprise doit bien sûr être correct, mais ensuite, on recherche la lisibilité pour que l’ensemble de l’équipe puisse le comprendre et le faire évoluer, aujourd’hui ou demain.

La performance n’a pas la même importance non plus : les besoins en performance sont contraints par les besoins de l’application et l’équilibre entre les coûts d’optimisation du code et les coûts matériels. Un premier regard rapide nous donne donc l’impression que les qualités nécessaires sont presque à l’opposé !

Qu’attend-on du développeur ?

Évidemment, ce n’est pas la conclusion à laquelle je souhaite vous emmener, mais cela me permet d’insister sur un point important. Les exercices d’algorithmie, inspirés de la programmation compétitive, n’ont en général rien à faire dans un processus de recrutement d’un développeur. On souhaite, à raison, que le candidat nous montre une capacité à écrire du code, mais on souhaite davantage voir un code lisible sur un problème plus concret ou plus proche du quotidien.

L’important à évaluer est la compréhension d’un code écrit par un autre, plus que sa compréhension d’algorithmes complexes. En bref, demander à un candidat d’écrire une boucle, quelques conditions et quelques cas simples du langage, comme de trouver le minimum dans une liste, est déjà largement suffisant comme complexité de problème pour avoir l’opportunité d’écrire du code et d’en discuter.

Ce qu’apporte la compétition de code au développeur

La programmation compétitive apporte d’autres atouts au développeur professionnel. Elle accompagne une maîtrise avancée des bases du langage et des structures de données. Cette maîtrise n’est pas forcément utile tous les jours, mais elle aide à prendre du recul sur certains problèmes du quotidien.

Exemple de problème de programmation compétitive 

Et si on regardait ensemble un problème de compétition de programmation en ligne ?

Voici l’énoncé tel que proposé lors du SWERC 2023-2024 :

Comme tous les joueurs de cartes, vous aimez triez votre main pour avoir une bonne vue de votre jeu. Comme tous les joueurs de cartes, vous alternez rouges et noires et à l’intérieur d’une couleur, vous triez vos cartes par ordre croissant.

Quel est le nombre minimum de mouvements à faire pour trier votre main ? Un mouvement consiste à prendre une carte et à la déplacer à un autre endroit.

Exemple :

Une seule couleur, on souhaite trier par ordre croissant :

On a fait deux mouvements : un avec la carte 3 de trèfle et un avec le valet de trèfle.

Les éléments de résolution 

Ici, on nous demande le nombre minimum de mouvements. Nous ne devons donc pas donner les mouvements eux-mêmes.

Le problème est simple à expliquer, mais sa résolution va nécessiter quelques étapes…

1.

La première étape consiste à bien comprendre le problème.

Le nombre minimal de mouvement de cartes nous incite à réfléchir sur les cartes qui doivent bouger. Ce n’est pourtant pas la bonne approche. Il faut se concentrer sur les cartes qui ne bougeront pas ! En effet, en bougeant une carte, on l’amène directement à sa « bonne » position. On a alors la relation :

Nombre de cartes total = nombre de cartes qui bougent + nombre de cartes qui ne bougent pas

En premier lieu, il faudra donc que l’on se concentre sur l’identification des cartes qui ne vont pas bouger : ce sont celles qui sont déjà dans le bon ordre dans notre main.

2.

La seconde étape est la définition de ce « bon ordre ».

Le sujet est flou sur cet ordre : on nous demande seulement les couleurs alternées et ensuite, en ordre croissant. 8 combinaisons de couleurs respectent cette alternance :

Cela nous fera donc 8 ordres à tester.

3. 

La troisième étape est de déterminer, pour un ordre donné, le maximum de cartes déjà « bien ordonnées ».

Fixons arbitrairement un premier ordre à tester. Par exemple : ♥ ♠ ♦ ♣

Nous pouvons maintenant donner un nombre à chaque carte :

Les cartes déjà dans le bon ordre sont celles qui forment une suite croissante (preuve laissée au lecteur). C’est plus facile de manipuler des nombres que des cartes ! Nous cherchons le maximum de nombres qui sont en ordre croissant dans notre liste de nombres.

 C’est une question déjà connue par les amateurs « éclairés » d’algorithmie. C’est le problème de la plus grande sous-séquence croissante (Longest Increasing Subsequence), appelée souvent LIS.

Le problème se résout par programmation dynamique (consultez cette vidéo YouTube pour des explications plus détaillées sur le sujet). Expliquons-en le principe et considérons notre ensemble dans lequel nous cherchons cette séquence :

10, 15, 7, 19, 2, 16

Nous allons parcourir l’ensemble des nombres et conserver les plus grandes séquences de chaque longueur. Pour être plus précis, nous allons conserver la valeur minimale du dernier élément de la séquence de chaque longueur, ce qui nous permet de ne conserver qu’une donnée et de les stocker dans un tableau.

Initialisation à -1 de notre tableau.

-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Première itération : le nombre 10.

On peut dire ici que la séquence de longueur 1 se finit au moins par 10. Notre tableau devient :

10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Seconde itération : le nombre 15.

On peut dire ici qu’une séquence de longueur 2 se finit au moins par 15, la séquence de longueur 1 se finit au moins par 10. Notre tableau devient :

10, 15, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Troisième itération : le nombre 7.

7 est plus petit que 10. On peut donc dire qu’une séquence de longueur 1 se finit au moins par 7, et qu’on ne peut pas construire de séquence de longueur 2 avec. Notre tableau devient :

7, 15, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Quatrième itération : le nombre 19.

Cela nous permet de construire une séquence de longueur 3 qui finit par 19.

7, 15, 19, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Cinquième itération : le nombre 2 va remplacer le 7.

2, 15, 19, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Sixième itération : le nombre 16 qui va remplacer le 19.

2, 15, 16, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, …

Généralisons : à chaque étape, on cherche l’emplacement où « poser » notre nouveau nombre, c’est-à-dire le plus petit nombre de notre tableau qui est plus grand que notre nouveau nombre. S’ils sont tous plus petits, on peut construire une séquence plus longue ! Cette recherche peut naïvement être effectuée en parcourant l’ensemble du tableau, mais on peut profiter d’une optimisation supplémentaire.

4.

La quatrième étape repose sur l’optimisation de la recherche dans le tableau.

Notre tableau est trié par construction. On peut donc chercher par dichotomie pour accélérer cette recherche. Le principe de la dichotomie est simple : si je suis dans un ensemble trié, je regarde au milieu de l’ensemble pour savoir si la valeur que je cherche est dans la première ou la deuxième moitié de mon ensemble. Je divise ainsi mon ensemble jusqu’à n’avoir que la valeur que je cherche.

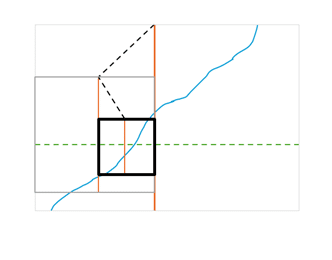
5. 

La cinquième étape est de passer à l’implémentation et de mettre ensemble l’ensemble des étapes.

Le nombre minimal sera :

 Nombre de cartes qui bougent = Nombre de cartes total – nombre de cartes qui ne bougent pas

Et le nombre de cartes qui ne bougent pas sera calculé pour chaque alternance possible de couleurs avec l’algorithme de plus longue séquence croissante optimisée.

Enfin, il ne faut pas oublier de vérifier son code sur des cas simples et de corriger les éventuelles erreurs !

Cet exercice est inspiré de l’exercice A du SWERC 2024 auquel a participé l’équipe Meritis en janvier dernier.

En conclusion, les exercices d’algorithmie ne reflètent pas la compétence et il ne faut pas les utiliser pour classer des candidats. La qualité de code, la lisibilité, la documentation, la maintenabilité sont de réels besoins du code professionnel qui ne doivent pas être sacrifiés sur la vitesse d’exécution ou d’écriture du code.

Les problèmes rencontrés en entreprise sont également très différents. Il ne faut pas pour autant nier les atouts de la programmation compétitive : la persévérance, la logique, la résolution de problèmes sont des compétences transverses très utiles, et la maîtrise des outils et du langage est une vraie compétence professionnelle.

Enfin, c’est un sport intellectuel, avec des communautés et de nombreux événements. Les rejoindre et y participer sont également une occasion d’apprendre, de progresser et de passer de bons moments.