La récursion terminale à la rescousse !

Posons le décor : vous êtes à un entretien. Tout se passe bien. Quand tout à coup, la fameuse question sur la récursivité arrive. Aucun souci pour le développeur que vous êtes, vous savez ce qu’est une fonction récursive. Vous implémentez donc une solution au problème posé. Et voici le résultat obtenu : Exception in thread « main » java.lang.StackOverflowError.

Que s’est-il donc passé ? Vous avez tout simplement « stacké » (empilé) trop d’informations. Stacké ? En français, Stack Overflow signifie « débordement de pile ». Sous-entendu la pile d’appel. La pile est une structure de données permettant de garder en mémoire plusieurs informations. Pour chaque fonction active (fonction appelée mais dont l’exécution n’est pas terminée), la stack garde en mémoire :

• ses paramètres
• ses variables locales
• l’adresse de retour de la fonction (grossièrement, où dans le code devra-t-on retourner après avoir exécuté la fonction)

Remarque : faire automatiquement le rapprochement entre StackOverflow et récursivité serait une erreur. Il existe d’autres cas où cette erreur peut provenir, comme par exemple l’utilisation de structures de données trop volumineuses pour la stack. Cet article se concentre juste sur un cas précis : la récursivité.

Comprendre l’empilement

Prenons le cas d’une fonction illustrant bien notre propos :

/**
  * A chaque appel récursif, cette fonction récupère la valeur du premier élément
  * de la liste puis rappelle la fonction avec 
  * la liste tronquée du premier élément
  */
def sum(arr: Array[Int]): Int = {
  val currentValue = arr.head
  if (arr.tail.isEmpty)
    currentValue
  else
    currentValue + sum(arr.tail) ← l'erreur qui vous aura été fatale
}

Dans le cas de la fonction sum, le point à retenir est que l’appel récursif n’est pas la dernière opération à être exécutée. En effet la dernière opération est l’addition de currentValue et du résultat de l’appel récursif. Tant que l’appel récursif n’a pas retourné sa valeur, la pile d’appel est obligée de garder en mémoire les variables locales, étant donné qu’elles sont susceptibles d’être utilisées plus tard dans la fonction. C’est la raison pour laquelle, à chaque appel récursif, de nouvelles données sont stockées en mémoire et donc “empilées”.

La récursion terminale pour quoi faire ?

La récursion terminale diffère de la récursion “classique” en deux points :

• l’appel récursif est la dernière instruction à être évaluée
• un accumulateur est passé à chaque appel et permet de “porter” le résultat temporaire de la fonction

Simplement exprimé, cela signifie que toutes les autres instructions ont été évaluées avant l’appel récursif, l’accumulateur peut être modifié en conséquence (dans notre cas, on additionne à la valeur en cours), puis on effectue l’appel à la fonction avec l’accumulateur mis à jour. La stack n’a plus de nécessité de garder des valeurs temporaires en mémoire, l’emplacement mémoire peut donc être réutilisé pour des évaluations ultérieures. Par exemple, on pourrait réécrire la fonction sum comme suit :

def sum2(arr: Array[Int], acc: Int = 0): Int = {
  val currentValue = arr.head
  if (arr.tail.isEmpty)
    currentValue + acc
  else
    sum2(arr.tail, currentValue + acc)
}

Dans le cas de sum2, l’appel récursif (quand il est nécessaire) est bien la dernière instruction, currentValue ajouté de acc étant évalué juste avant. A noter que la façon d’implémenter sa fonction récursive ne suffit pas à éliminer le problème d’empilement.

Et la “tail-call optimization” ?

Il est nécessaire de bien distinguer ce qu’on appelle la tail-recursion (concept énoncé ci-dessus) de la tail-call optimization. Si la première dépend entièrement du développeur, la seconde dépend, elle, du compilateur et donc du langage utilisé.

Par exemple, en Scala, le problème est résolu partiellement, cette optimisation n’étant possible que dans les cas suivants :

• la fonction est finale (le compilateur sait qu’elle ne sera pas “overriden”)
• la fonction est une fonction locale (“nested”)

Pour illustrer, prenons le cas suivant :

class Fact {
  def factorielle(n: Int, acc: Long = 1): Long = {
    if(n == 0) acc else factorielle(n-1, acc*n)
  }
  final def factorielle2(n: Int, acc: Long = 1): Long = {
    if(n == 0) acc else factorielle2(n-1, acc*n)
  }
  def factorielle3(n: Int): Long = {
    def factorielle(n: Int, acc: Long = 1): Long = {
      if(n == 0) acc else factorielle(n-1, acc*n)
    }
  
    factorielle(n)
  }
}

Dans cet exemple, seules les fonctions factorielle2 et factorielle3 seront optimisées. Le code compilé de factorielle2 et factorielle3 ne contiendra plus d’appel récursif (remplacé par un appel itératif) permettant ainsi d’éviter l’empilement et le débordement de la pile.

Remarque : il est intéressant de noter que depuis la version 2.8 de Scala, l’annotation @tailrec permet de s’assurer qu’une fonction récursive sera bien optimisée par le compilateur. C’est un gage de sécurité supplémentaire pour le développeur. Dans le cas où la méthode annotée ne peut-être optimisée (fonction non récursive, méthode non finale et non locale …), alors la compilation échouera.
 A l’inverse, le compilateur Java ne supportant pas cette optimisation, il sera impossible d’éviter le débordement par le biais de la récursion terminale. Il ne tiendra alors qu’à vous de trouver une façon de réécrire votre fonction afin d’éviter l’empilement. Par ailleurs, la taille de la stack est configurable par les options de la JVM (Xss ou XX:ThreadStackSize). Dans certains cas il peut suffire d’augmenter l’espace disponible, mais ce ne doit être qu’une solution de secours, car elle peut amener à des dérives (éviter le “ça tourne mal ? Attend, j’alloue plus de RAM !”).

Le choix de la récursivité

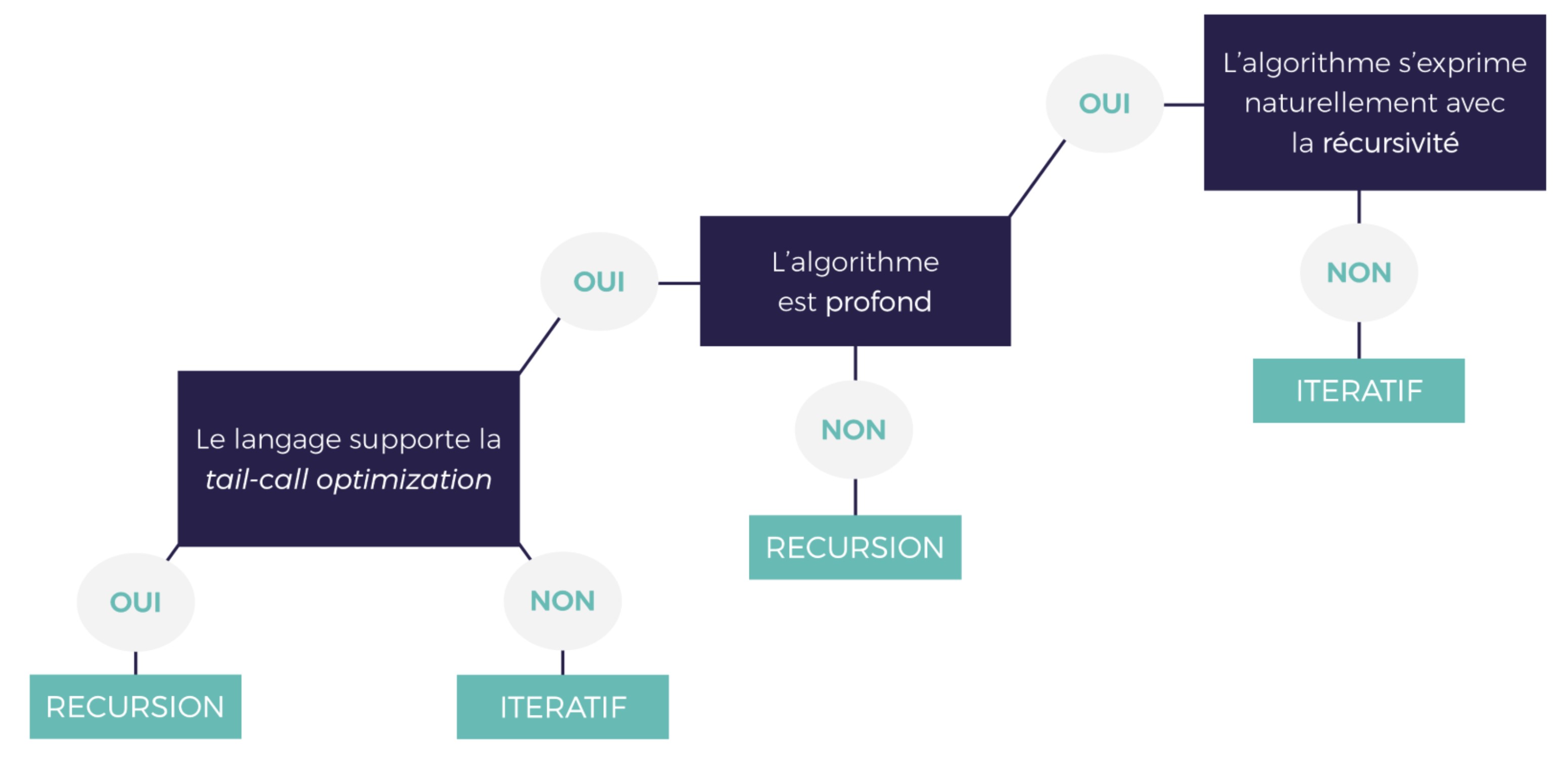
Afin de choisir entre récursivité ou itération lors de l’implémentation d’une fonction, il utile néanmoins de se poser trois questions.

La première : l’algorithme s’exprime-t-il naturellement avec la récursivité ? Il est généralement assez facile d’y répondre. Par exemple, la traversée d’un arbre semble naturelle par le biais de la récursivité. Faire la somme des valeurs d’une liste semble un peu plus retor. Si la réponse est non, pourquoi prendre des risques ? Préférez l’itération.

Deuxième question à se poser : l’algorithme est-il profond ? S’il s’exprime effectivement simplement avec la récursivité, reste à savoir si une implémentation avec récursion terminale est nécessaire. En effet, il serait inutile d’ajouter une variable supplémentaire (l’accumulateur) si dans tous les cas la fonction n’est pas profonde, c’est à dire que le nombre d’appels à la fonction est “faible” ou “tolérable”). Ce peut être le cas s’il existe une condition d’arrêt restreignant l’exécution de votre fonction. Ou si votre fonction arrive rapidement à sa phase terminale. Dans le cas où l’algorithme n’est pas profond, la récursivité (terminale ou non) semble appropriée.

Autrement il reste une dernière question à se poser. Le langage supporte-t-il la tail-call optimization ? Si l’algorithme est effectivement profond et qu’il semble naturel de l’implémenter avec la récursivité, il y a potentiellement un risque. Premièrement, la récursivité terminale devient un must. Ensuite, il est nécessaire de s’assurer de la prise en charge de la tail-call optimization par le langage d’implémentation. De cette vérification dépendra le choix “itératif” / “récursivité”.

 

Un principe à connaître

En définitive, la tail-recursion est un principe à connaître dès lors que l’on souhaite implémenter un algorithme récursif. Il permet, si le langage supporte la tail-call optimization, d’assurer au développeur que le code s’exécutera sans causer de problème de pile. Dans le cas contraire ne reste que la solution de “dé-récursifier” en se basant sur des concepts itératifs.