À chaque crise financière, ce sont bien souvent l’ensemble des acteurs économiques qui trinquent. Or, tous les secteurs devraient pouvoir mesurer leur exposition aux risques auxquels les soumettent les marchés financiers. Ce sont les banques et les assurances qui font office de pionnier en la matière, compte-tenu de leurs activités. Or plusieurs modèles s’opposent. Si la Value at Risk (VaR) a longtemps eu les faveurs des observateurs, celui de l’expected shortfall tend désormais à s’imposer.
C’est dans l’industrie de l’assurance que la “Value at Risk” (VaR) est née. Il faut attendre les années 90 pour que cette mesure soit formellement définie et qu’une banque, Morgan Stanley, se dote d’une méthodologie officielle l’utilisant pour mesurer globalement son exposition au risque. Ces “Risk Metrics” furent plus tard la première véritable méthodologie commune aux établissements bancaires soumis aux risques de marchés. À tel point que la VaR est devenue en 2004 l’une des recommandations de Bâle II, malgré les critiques dont elle faisait déjà l’objet.
La Value at Risk comme mesure du risque
Alors, concrètement, de quoi parle-t-on quand on parle de VaR. La VaR vise à quantifier la perte maximale d’un investisseur exposé à un actif X étant donné un degré de confiance α∈[0;1] et un horizon temporel T. Autrement dit, il mesure la quantité C telle que j’ai une probabilité 1-α que mon exposition au risque me coûte plus de C sur T jours. En termes mathématiques, cela s’écrit :
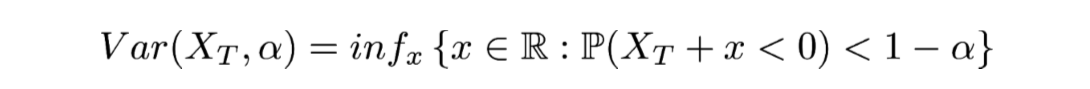
On notera que la notion de VaR est directement liée à celle de quantile puisqu’il s’agit de l’opposé du quantile de niveau . En fait, le calcul de la VaR nécessite de déterminer la distribution des risques possibles. Ce qui paraît être un bon début si l’on veut obtenir une mesure du risque efficace.
Bien entendu, ce qui vaut pour un actif doit en réalité être appliqué à l’ensemble des facteurs de risques d’une même institution afin de déterminer la VaR. Une fois ces facteurs de risque déterminés, on peut passer à la simulation. Pour la calculer, il existe plusieurs approches :
- une approche paramétrique (la méthode variance/covariance par exemple),
- une approche Monte-Carlo (qui requiert un grand nombre de simulation),
- une approche historique.
L’inconvénient des deux premières c’est qu’elles font des hypothèses sur la distribution des pertes. En général, on suppose qu’elles suivent une loi normale. Or on sait depuis les travaux de Mandelbrot que c’est en général faux.
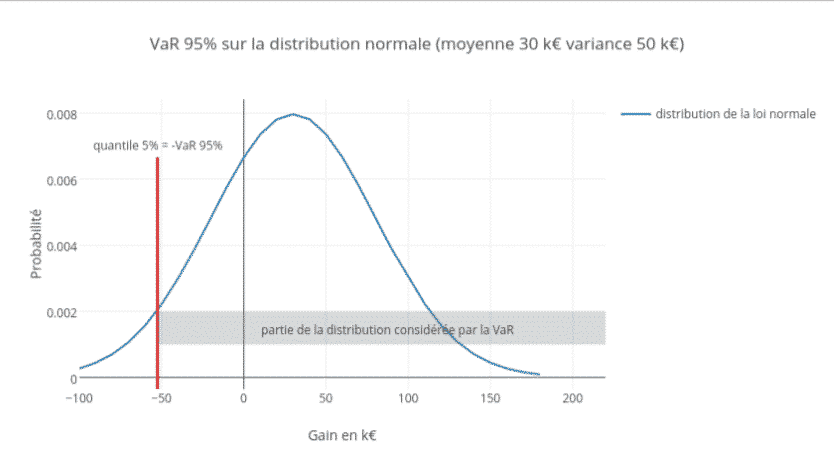
Avec ce modèle VaR, il est impossible de modéliser les risques de marché les plus violents.
Pour faire simple, selon la loi normale, les événements se situant dans la queue de la distribution, là où les pertes sont les plus fortes, sont statistiquement trop peu représentés sous cette loi. Impossible dans ces conditions de modéliser correctement les risques les plus violents rencontrés sur les marchés financiers. C’est le phénomène des queues épaisses.
Il existe une définition mathématique précise de ce que sont les queues épaisses des distributions de probabilités, ou queues lourdes. Un bon exemple de comparaison avec la loi gaussienne est la loi de Student,ou t-distribution,car elles ont toutes les deux cette forme caractéristique de cloche. On pourra aussi voir la notion de Kurtosis qui est une notion importante de classification et d’analyse des distributions de probabilités. On trouve aussi sur Wikipédia des graphiques comparant la loi normale et la distribution de student.
On voit que quand le degré de liberté est faible, les éléments les plus extrémaux, c’est à dire les plus à gauche et les plus à droite, seront nettement plus fréquents avec la loi de student. C’est une des observations les plus importantes à mon sens que l’on retrouve dans le document sur Mandelbrot. On l’appelle le syndrome de Noé.
L’approche historique, certainement la plus utilisée, agrège pour sa part des données passées récupérées sur les marchés. On utilise les variations observées pour les appliquer à l’état de départ du marché afin de calculer les pertes de nos facteurs de risque. Cette approche permet notamment d’inclure des scénarios hypothétiques basés sur des avis d’expert.
L’intérêt de la VaR réside en ce qu’elle a permis de poser une méthodologie définissant une base de réflexion, laquelle a fait émerger des axes de recherche sur la mesure du risque. Cela a conduit, par exemple, à la notion de mesure cohérente du risque. Il s’agit d’une définition mathématique qui, sous certains aspects, est assez complexe mais très pertinente car elle permet de demander à une telle mesure d’être sous additive. En d’autres termes : ∀Z_1,Z_2 deux variables aléatoires, μ est une mesure sous additive si :
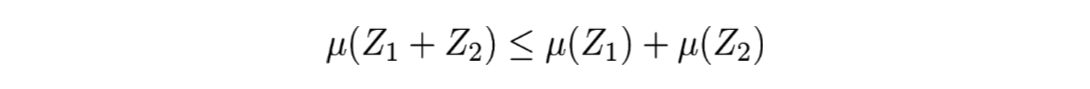
Tout l’intérêt de cette formule est, lorsque μ représente une mesure du risque, qu’elle traduit la diversification du risque. On peut ainsi énoncer qu’un portefeuille composé de deux actifs risqués similaires (mais différents) est moins risqué qu’un seul portefeuille composé d’un seul de ces risques. Mais l’inconvénient est que la VaR n’est pas sous-additive. En effet, si la variable aléatoire suivante :
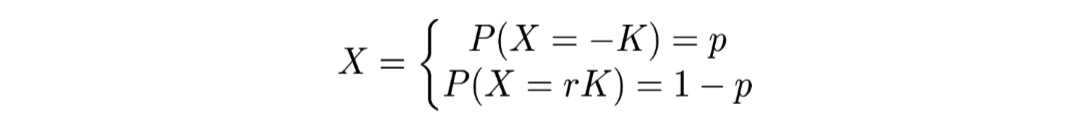
Cela représentant un actif dans lequel on perd le capital investit K avec une probabilité de p et ou on récupère le capital investit en faisant un gain de rK avec une probabilité de 1-p. Ici K et r sont des variables de ℝ+ et p est compris entre 0 et 1. Dans ce cas si p≤α alors la Value at Risk de X avec un niveau α est -rK.
Si on considère maintenant un portefeuille composé à parts égales de deux actifs suivants cette loi, on obtient que le portefeuille suit la loi suivante :
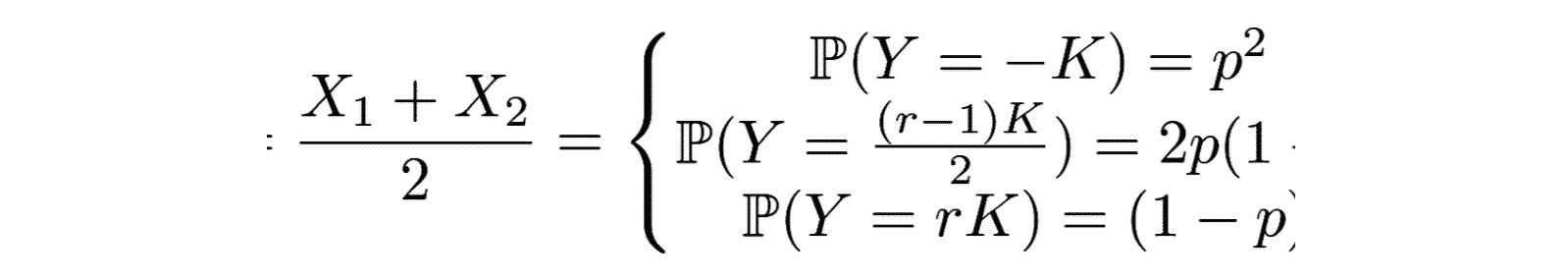
Ici la variable aléatoire, somme de deux variables aléatoires indépendantes suivant une loi de Bernoulli, est une variable aléatoire suivant une loi binomiale. Donc si α est compris entre p^2 et p^2+2p(1-p) comme pour α=1% et p=0.9%,
on a :
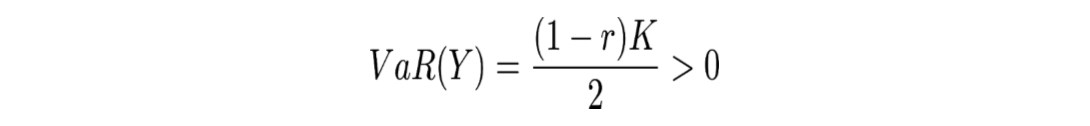
alors que :
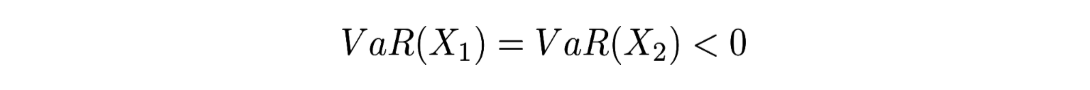
Cela illustre bien que la VaR n’est pas sous-additive et donc ne prend pas correctement en compte la diversification du risque.
Une autre critique de la VaR repose sur l’objet même de la mesure. Lorsque l’on dit que la VaR à 1% d’un portefeuille est 1 million d’euros, on dit que la probabilité de faire des pertes supérieures à 1 million est de 1%. Mais que se passe-t-il dans les 1% qui reste ? Ce sont les évènements de la queue de la distribution et on sait qu’ils peuvent être particulièrement violents, disons une perte de 1 milliard par exemple. Dans ce cas-là même si la VaR peut sembler acceptable, il existe au moins un événement possible qui ne l’est pas.
Pour bien comprendre comment fonctionne le calcul de la VaR donnons-nous un petit exemple simple. Voici un tableau qui donne la probabilité de la répartition des gains d’un outil financier :
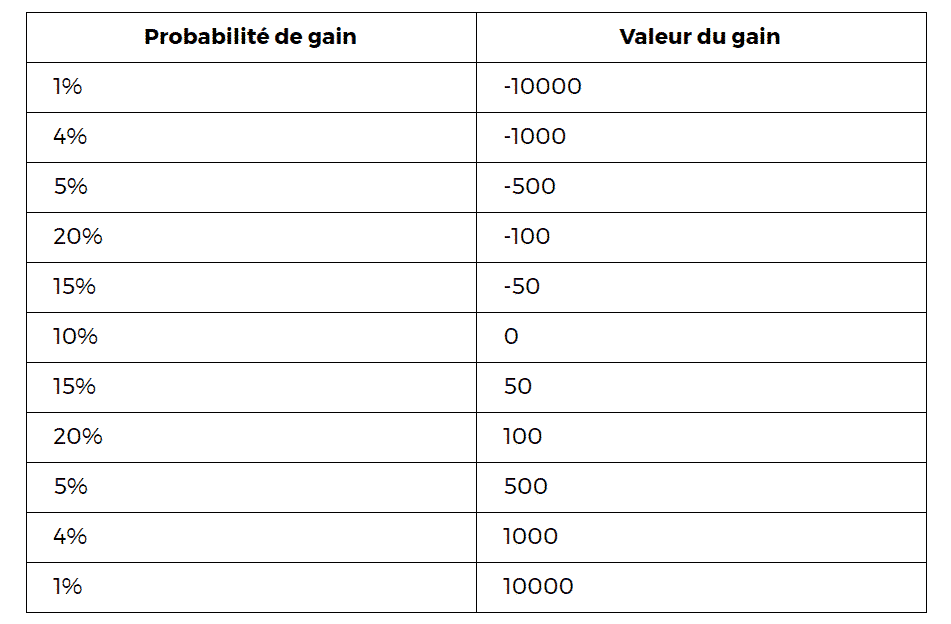
Si l’on prend la VaR 99% on obtient 10000, tandis que pour la Var 95% on obtient 1.000.
L’expected shortfall, une mesure du risque de queue
Depuis que la VaR est apparue, le concept de mesure du risque a fait du chemin. A tel point que la Fundamental Review of the Trading Book (FRTB) publiée en 2016 suggère carrément de remplacer la VaR par l’expected Shortfall.
Si on prend la définition de John Hull (dans le glossaire ici par exemple), l’expected shortfall est la perte probable quand on se trouve dans les α% scénario de la queue de la distribution des pertes. Pour être tout à fait précis, il faudrait également préciser l’horizon temporel comme pour la VaR. C’est ce qu’exprime cette formule :
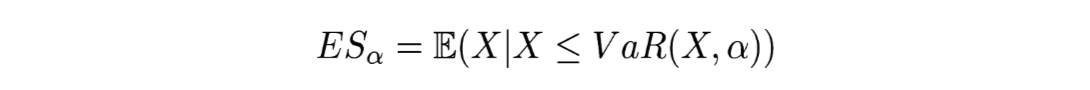
Il s’agit de l’espérance conditionnelle des pertes considérant un niveau de VaR. Une autre façon de l’écrire est la formulation suivante :
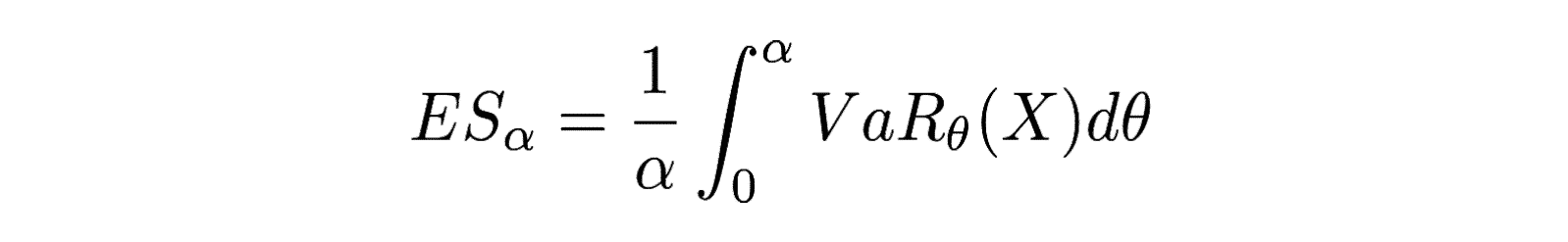
Personnellement je trouve les deux formulations intéressantes. Mais plus simplement on peut aussi dire que l’expected shortfall est la moyenne des pertes subies lors d’un choc qui n’apparaît que dans les α% pire(s) cas. De plus l’expected shortfall est toujours supérieure à la VaR.
Si on reprend les données de l’exemple utilisé pour la VaR, on obtient pour l’ES 99% une valeur de 10000 et pour l’ES 95% :
((1/100)10000 + (4/100)1000)/(5/100) = (10000+4000)/5 = 2800.
On remarque que la valeur obtenue pour l’ES 95% est nettement plus grande que celle obtenue pour la VaR 95%. En fait, l’expected shortfall, à un seuil donné, est toujours supérieure à la VaR au même seuil. C’est assez intuitif puisque l’expected shortfall est une moyenne des pertes se situant au delà de la VaR.
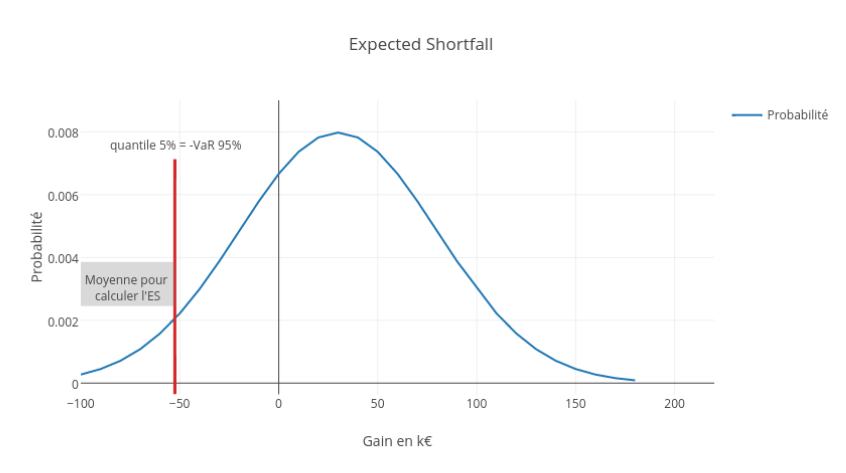
Il existe sous certaines conditions plusieurs autres définitions mathématiques équivalentes. L’expected shortfall est d’ailleurs désignée par d’autres noms dans la littérature relative à la gestion des risques (CVaR, Expected Tail Loss).
L’important ici n’est pas vraiment les définitions, même si elles sont utiles, ce qu’il faut retenir c’est que l’on cherche à corriger deux points faibles de la VaR :
- prendre en compte la queue de la distribution
- avoir une mesure cohérente du risque
C’est cette mesure qui est désormais préconisée par la FRTB. Les horizons de liquidité à prendre en compte sont divers et fonction du type de risque. Quant au seuil de confiance il est préconisé d’utiliser 97,5%. Il ne reste plus qu’à calculer cette mesure du risque… tous les jours… et sur l’intégralité des portefeuilles de trading des banques. Une broutille en somme.
Le calcul effectif et ses conséquences
Comme pour la VaR, on peut utiliser les trois approches :paramétrique, historique et Monte-Carlo. On pourra trouver un bestiaire mathématique de ces modèles ici. On trouve également à la fin du document des références à des logiciels permettant ces calculs.
L’approche paramétrique est riche en modèles. On utilise dans ce cas des familles de distribution que l’on peut ajuster en utilisant des paramètres. Il s’agit ensuite de trouver les paramètres optimaux dans le sens où la distribution obtenue caractérise aux mieux un ensemble d’observations passées. Si cette méthode est relativement rapide, elle crée une dépendance forte avec un modèle statique (un élément d’une famille de distribution caractérisé par quelques paramètres). Elle peut donner de bons résultats dans les cas où l’on dispose des bonnes données permettant de définir un bon jeux de paramètres.
La méthode Monte-Carlo nécessite également des hypothèses sur la distribution des pertes afin de procéder à des tirages. Cependant, elle permet de générer beaucoup de trajectoires et donc de travailler avec des ensembles de données plus grands. Malheureusement, la génération est très pénalisante en temps de calcul. Et ce d’autant plus qu’il faut en général un grand nombre de trajectoires pour converger vers un résultat acceptable.
La méthode historique se révèle plus rapide que celle de Monte-Carlo et moins dépendante de paramètres comme les méthodes paramétriques. Elle a néanmoins comme inconvénient d’être très fortement dépendante de la qualité des données et des scénarios passés retenus.
On se trouve donc dans un dilemme de numéricien devant choisir entre plusieurs méthodes présentant chacune des inconvénients importants. C’est souvent la méthode historique qui est choisie.
De l’importance des données
Actuellement, les données historiques permettent de définir des notions de conditions de stress.C’est le cas dans Bâle 2.5 pour la SVaR ou la FRTB pour l’expected Shortfall. Il s’agit de créer une forme de renormalisation des mesures de risque afin d’éviter qu’elles ne soient trop liées aux conditions de marché au moment du calcul. Pour cela, on utilise les données d’une période de stress d’au moins un an, période de référence que l’on va utiliser pour ajuster la valeur obtenue dans le modèle choisi pour le calcul.
Il va sans dire que la qualité et la quantité des données jouent un rôle essentiel . En effet, il faut des données qui concernent non seulement toutes les composantes des risques identifiés au sein de l’institution mais qui couvrent aussi des périodes de temps représentatives. De plus, il faut que ces périodes contiennent elles mêmes suffisamment de données, c’est l’échantillonnage. Et finalement il faut un grand nombres de scénarios pour obtenir un résultat satisfaisant.
Pour des banques dont le poids est important sur le marché avec des périmètres très larges, typiquement les banques identifiées comme systémiques, le volume des données est considérable. Il faut également prendre en compte le fait que le calcul en lui même produit un grand nombre de variables intermédiaires qu’il faut souvent stocker pour des besoins ultérieurs (les market data choquées par exemple).
Le big data à la rescousse, le stockage en suspens
Le big data peut ici intervenir de façon intéressante et il y a fort à parier qu’il y a là un terreau particulièrement fertile à son développement. Mais l’étendue des difficultés ne s’arrête pas au stockage de la données, il faut aussi pouvoir la manipuler, la transformer puis l’exploiter. Pour cela il est tout à fait possible de faire appel à un pattern comme le map/reduce et des outil comme Spark. De mon point de vue, la partie map peut intervenir de la même façon que la vectorisation que l’on croise dans les librairies de calcul vectoriel. En se basant sur ce paradigme, il est possible de bâtir une architecture cible en utilisant ces outils, data lake et autre noeud hadoop, et les librairies de pricing utilisées par les acteurs du marché.
En somme, une véritable révolution du système d’information s’impose dans le cadre des réglementations du risque. Espérons que cela nous préserve au mieux des tempêtes provoquées par les crises.
ANNEXE
Les propriétés d’une mesure cohérente du risque sont :
- L’invariance par translation :
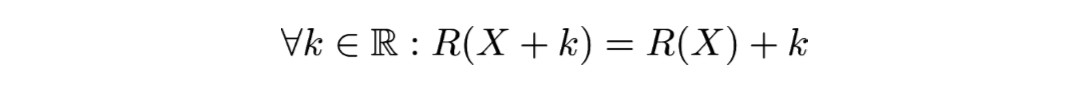
- L’homogénéité :
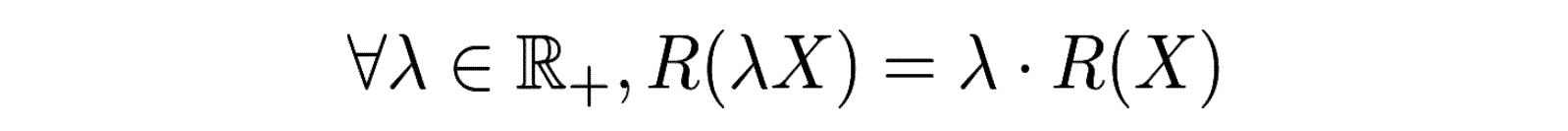
- La monotonicité :
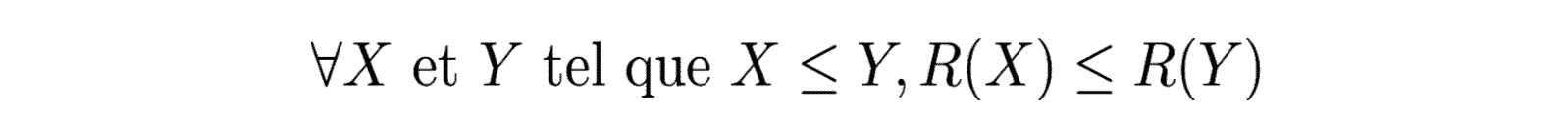
- Invariance en loi :
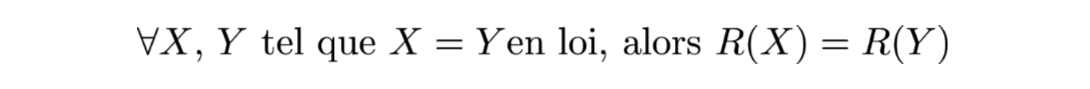
- Sous-additive :
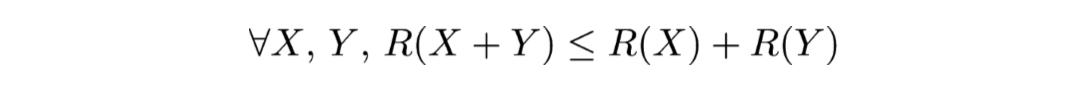




Vos commentaires
Très bon article, merci beaucoup !
Un excellent articule !
Merci
Excellent article. Simplement, 2 toutes petites observations:
1) Dans la présentation de la VaR, la distribution Gaussienne présentée n’est pas de variance 50, mais d’écart-type 50
2) Plutôt que de présenter la valeur de la VaR comme la borne inférieure de l’ensemble des gains possibles pour un « degré de confiance » donné (vocabulaire ds statisticiens classiques), il me semble qu’il est plus « intuitif » de dire que c’est la plus grande perte possible pour les x% ds pires scénarios possibles (mon « x » est votre (1-), bien sûr). On doit convenir que c »est exactement la même chose (et vous dites dans le texte « presque » cela), mais d’un point de vue pédagogique lorsqu’on s’adresse au commun des mortels (et aux professionnels traditionnels de la finance!)…on est mieux compris. Mais c’est mineur. Bravo pour ce blog!
Excelllent. Parfaitement expliqué. Merci beaucoup !
Merci pour ce retour.
Bonjour,
Vous dites que « Si l’on prend la VaR 99% on obtient 10000, tandis que pour la Var 95% on obtient 1.000. »
Pourriez-vous m’expliquer pourquoi?
J’ai un exercice de calcul de VaR historique à résoudre avec un tableau reprenant des données comme le vôtre et je n’arrive pas à comprendre comment faire pour la calculer.
Merci d’avance pour votre aide