Il existe différents modèles d’évaluation des options. Ils permettent d’ajuster votre stratégie trading ou votre portefeuille ! On vous présente dans cet article, deux des méthodes les plus connues : la méthode binomiale et la méthode de Black and Scholes.
Les modèles d’évaluation des options sont des modèles mathématiques qui utilisent certaines variables pour calculer la valeur théorique d’une option. Ces différentes méthodes prennent en compte notamment la valeur intrinsèque et la valeur temps attachées aux options. De cette manière, grâce à cette estimation, les traders et/ou les investisseurs peuvent ajuster leurs stratégies de trading et leurs portefeuilles. Parmi les méthodes d’évaluation d’options les plus connues, nous retrouvons la méthode binomiale et la méthode de Black and Scholes.
1. Qu’est-ce qu’une option ?
Une option est un contrat entre deux contreparties qui donne à l’une des deux le droit, et non l’obligation, d’acheter ou de vendre l’actif sous-jacent (actions, devises, matières premières, etc.) pendant une période donnée et à un prix convenu à l’avance. On compte deux grands types d’options : les calls et les puts.
L’option d’achat (call)
Il s’agit d’un contrat d’option qui donne le droit à son détenteur d’acquérir l’actif sous-jacent pendant une période donnée et à un prix convenu à l’avance. L’exercice de ce droit n’est en aucun cas une obligation. Ci-dessous, retrouvez les schémas de pay-off.
Achat d’une option d’achat (long call)
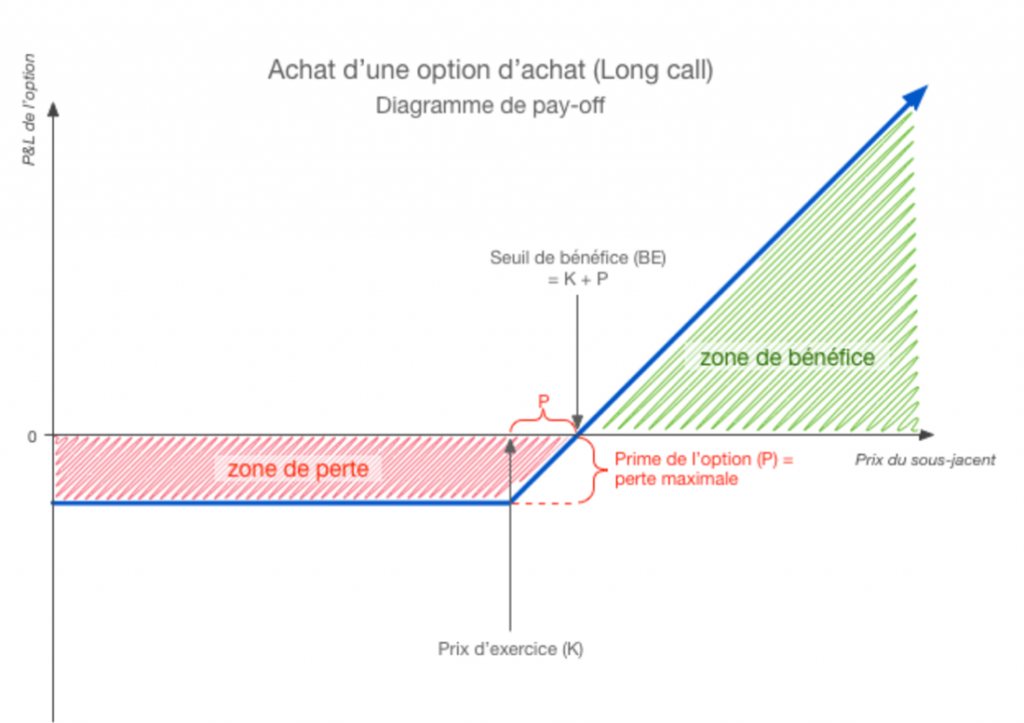
Vente d’une option d’achat (short call)
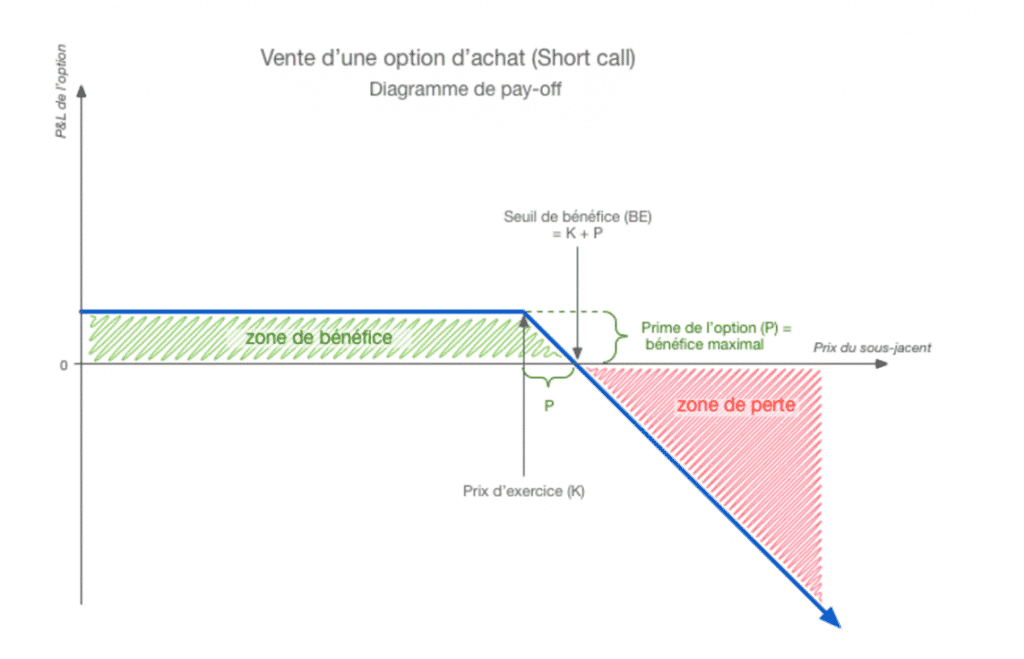
L’option de vente (put)
Il s’agit d’un contrat d’option qui vous donne le droit de vendre l’actif sous-jacent pendant une période donnée et à un prix convenu à l’avance. L’exercice de ce droit n’est en aucun cas une obligation. Ci-dessous, retrouvez les schémas de pay-off.
Achat d’une option d’achat (long call)
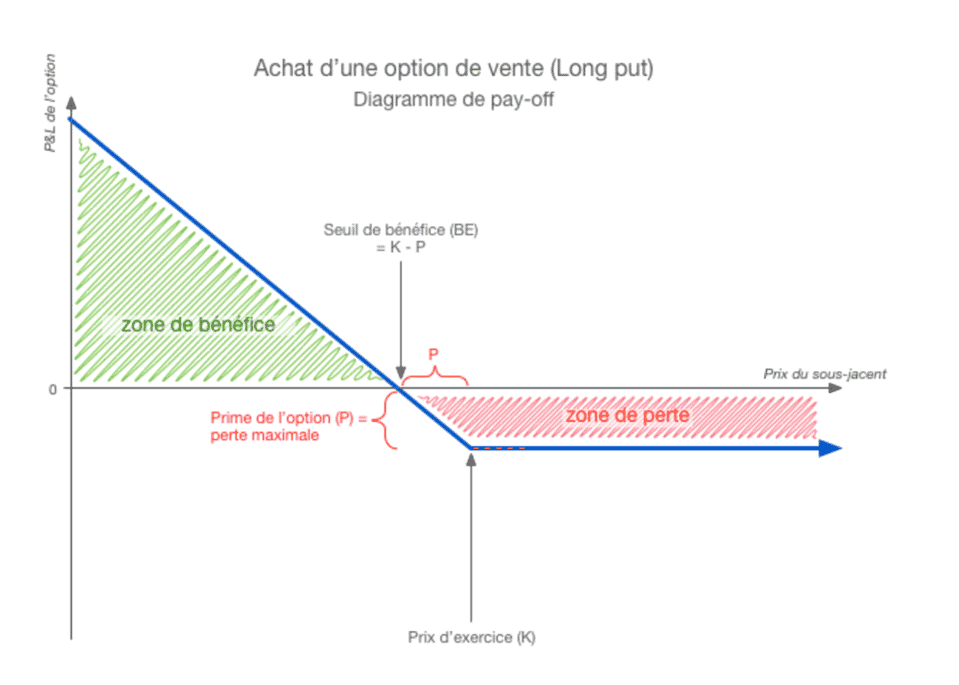
Achat d’une option d’achat (long call)
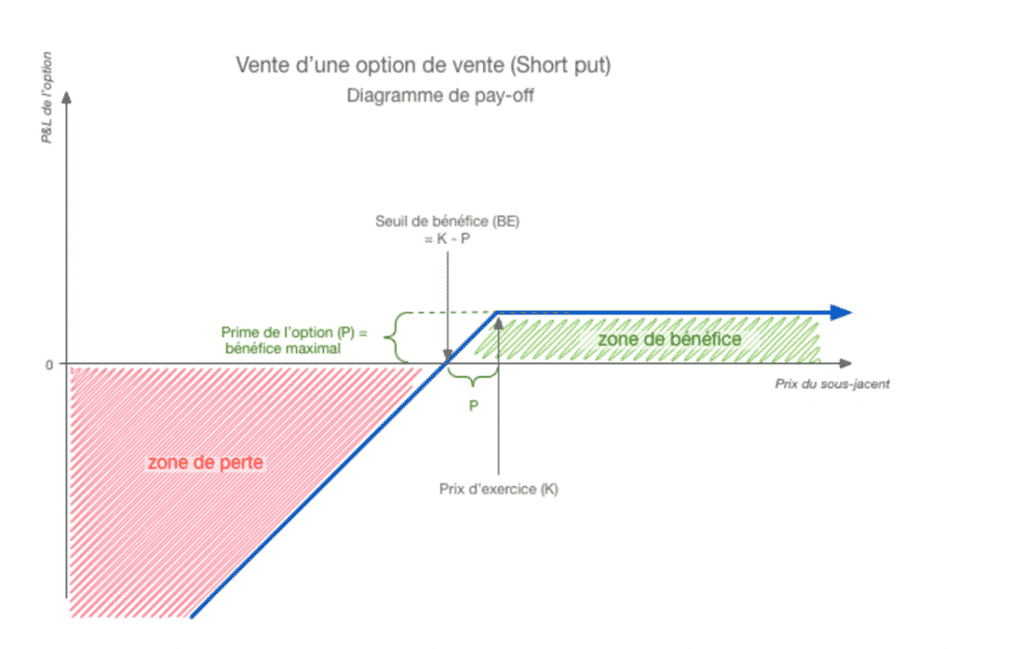
Nous pouvons également différencier les options américaines des options européennes :
- Les options européennes ne donnent la possibilité d’exercer son droit qu’à la date d’échéance de l’option.
- Les options américaines peuvent être exercées à tout moment entre la date d’achat et la date d’expiration.
2. Comment évolue une option ?
Le prix de l’option, c’est-à-dire la prime, varie en permanence. En effet, la prime varie en fonction du prix du sous-jacent (action, indice, devise, matière première, etc.), mais également en fonction de l’offre et de la demande.
Il est bon de noter que cette prime est théoriquement composée de deux éléments :
- La valeur « intrinsèque » qui représente le profit qui serait perçu immédiatement si l’on décidait d’exercer l’option ;
- Et la valeur « temps » qui s’ajoute à la valeur intrinsèque.
Une option possède donc un prix qui fait l’objet d’un calcul spécifique prenant en compte plusieurs paramètres :
- Le cours de l’actif sous-jacent : une hausse (réciproquement baisse) du cours de l’actif sous-jacent fait augmenter mécaniquement la valeur de l’option d’achat et donc fait perdre de la valeur à l’option de vente (et vice versa).
- Le prix d’exercice de l’option (strike) : cette variable affecte fortement la valeur de la prime de l’option. En effet, sa valeur intrinsèque dépend directement de la position du strike par rapport au prix de l’actif sous-jacent. Qui plus est, le strike a également une influence sur la valeur temps : plus le strike est proche du prix de l’actif sous-jacent, plus la probabilité que l’option soit exercée est importante.
- La durée de l’option : plus la maturité de l’option est éloignée dans le temps, et donc possède une durée de vie importante, plus les probabilités de variation des cours de l’actif sous-jacent sont grandes et les possibilités de gains également. Ainsi, lorsque la durée de vie d’une option est élevée, la prime qui lui est associée s’en trouve donc majorée. À l’inverse, la valeur d’une option diminuera au fur et à mesure que l’on approche de l’échéance de l’option.
- Les taux d’intérêt : dans le cas d’une option d’achat où l’actif sous-jacent est une action, plus le taux d’intérêt est élevé, et plus l’option sera chère (et vice versa pour les options de vente).
- Le dividende : le détachement d’un dividende engendre une perte de valeur de l’action. Cela aura pour conséquence une appréciation de la valeur d’une option de vente avant le versement du dividende et, inversement, la diminution de la valeur d’une option d’achat. Dans le cas d’une option de type américaine, son détenteur pourra exercer son droit d’achat juste avant le détachement du dividende. Cela lui permettra de ne pas être affecté par la baisse de la valeur de l’option (du fait de ce détachement). A contrario, le détenteur d’une option de type européenne sera, quant à lui, bloqué jusqu’à l’échéance de l’option.
- La volatilité : La volatilité représente la variation de la valeur d’un produit financier et traduit, par conséquent, le risque qu’un actif financier perde de la valeur. Dans le cas où l’actif sous-jacent est une action, un panier d’actions ou un indice, plus ces derniers évoluent, plus les primes des options d’achat et de vente seront élevées.
La probabilité « risque neutre »
Avant d’aborder les différents modèles d’évaluation des options, il est important de définir le concept de probabilité « risque-neutre », qui est largement utilisé dans l’évaluation des options et peut être présent au sein de différents modèles.
La probabilité « risque neutre » représente la probabilité que le prix d’un actif soit égal à la somme des flux futurs générés attendus. Ce concept repose sur deux hypothèses principales :
- La valeur actuelle d’un actif est égale à son gain attendu actualisé au taux sans risque ;
- Il n’y a pas d’opportunités d’arbitrage sur le marché.
L’avantage de la probabilité risque neutre est qu’une fois celle-ci calculée, elle peut être utilisée pour fixer un prix à chaque actif, en s’appuyant sur les revenus futurs attendus.
La probabilité risque neutre reste théorique puisque les revenus attendus s’ajustent à l’aversion de chaque individu au risque. L’acception « risque neutre » signifie donc qu’aucune prime n’est attribuée à la prise de risque.
3. La méthode binomiale d’évaluation des options
Le modèle binomial est un modèle très intuitif pour comprendre comment « pricer » la valeur d’une option.
Ce modèle suppose que le prix de l’actif sous-jacent peut être approché par un processus binomial, c’est-à-dire qu’il évolue à la hausse de (u) ou à la baisse de (d) sur chaque intervalle de temps.
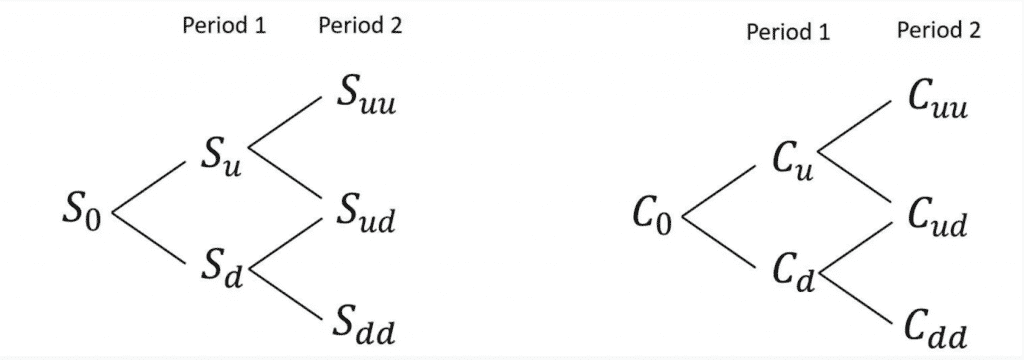
Par souci de clarté, nous présenterons ce modèle sous une version à une période donnée. Ainsi, on considère que le prix de l’actif sous-jacent va, soit monter (u), soit descendre (d) durant cette période. Ensuite, nous pourrons calculer le gain de l’option selon ces différents scénarios, puis actualiser ces derniers afin de trouver la valeur de cette option.
Construction de l’arbre
Les paramètres du modèle sont les suivants :
- Le prix de l’actif (S) ;
- Le prix d’exercice (K) ;
- La volatilité annualisée (𝜎) ;
- La maturité (t) ;
- Le taux d’intérêt sans risque (r).
En partant de la figure 1 et du prix de base , le facteur d’évolution vers la hausse durant la période 1 est « u » et le facteur d’évolution vers la baisse est « d ». Ces deux facteurs, qui obéissent à une logique brownienne géométrique, sont calculés par les formules suivantes :
u= e^(σ√δt) d= e^(-σ√δt)
Avec :
δt= Intervalle de temps entre deux nœuds
σ= Volatilité annualisée
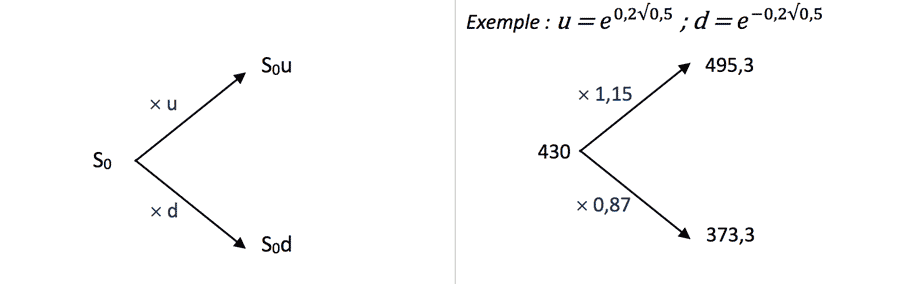
Construction des pay-off
Les nœuds terminaux de l’arbre des prix représentent les différents scénarios de prix auxquels le trader et/ou l’investisseur fera face à la maturité. Dans chacune de ces situations, selon que le prix du marché est favorable ou défavorable au prix d’exercice, il choisira ou non d’activer son option. Nous obtenons ainsi les pay-off possibles à la maturité : ils sont positifs lorsque l’option est activée et nuls lorsque l’option n’est pas activée.
Pour connaître le prix de l’option, nous construisons l’arbre des pay-off par induction rétrospective. En d’autres termes, le pay-off de chaque nœud intermédiaire est constitué par l’espérance actualisée des pay-off des deux nœuds suivants :
E=[p× 〖Pay off〗_1+(1-p)×〖Pay off〗_2 ] e^(-rδt)
Selon sa définition, la probabilité risque neutre indique que la hausse et la baisse ont les mêmes chances de se réaliser. De ce fait, nous obtenons :
p=(e^rδt-d)/(u-d)
Prenons le cas d’une option d’achat européenne avec les caractéristiques suivantes :
- Le prix de l’action : 60 USD ;
- Le prix d’exercice de l’option : 62 USD.
Et les paramètres suivants :
- u = 1,1 ;
- d = 0,9 ;
- r = 9 % ;
- T = 0,25 %.
Nous obtenons l’arbre suivant :
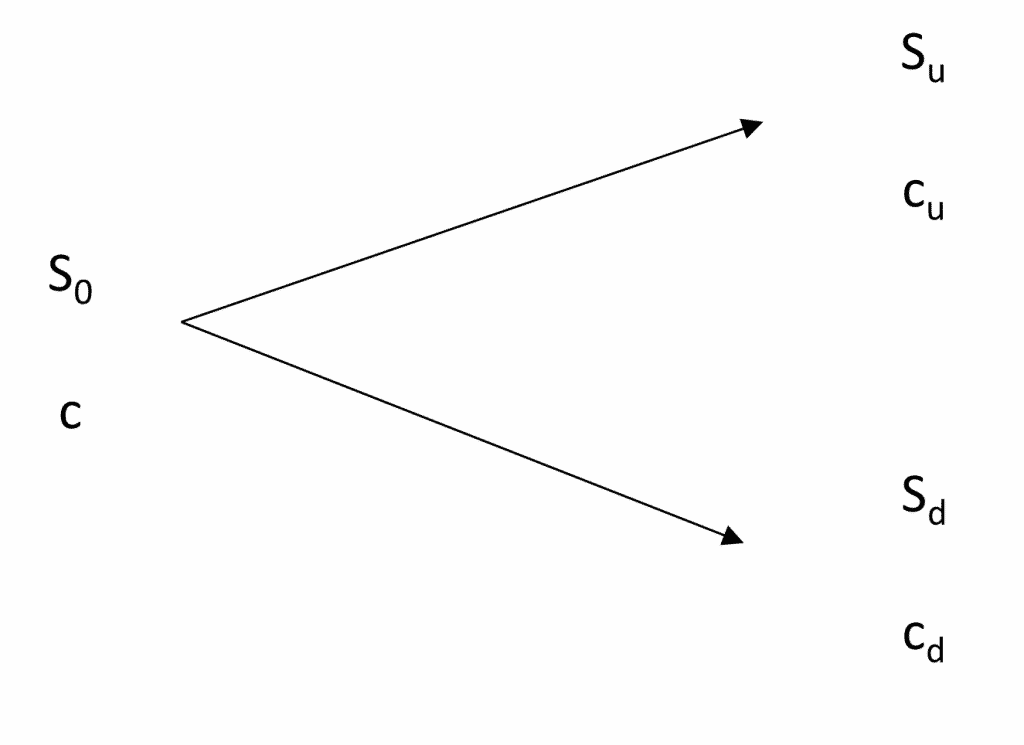
À partir des informations ci-dessous, nous obtenons :
p=(e^rδt-d)/(u-d)=(e^(0,09×0,25)-0,9)/(1,1-0,9)=0,6138
Ainsi, le but est de trouver la valeur du call C. Pour cela, nous devons trouver les valeurs de C_u et C_d.
Calcul de C_u :
Pour déterminer C_u nous devons déterminer le prix de l’actif sous-jacent en cas de hausse u :
S_u=S_O×u=60×1,1=66
Donc la valeur de est de :
C_u=MAX[0,S-K]=MAX[0,66-62]=4
Calcul de C_d :
Pour déterminer C_d nous devons déterminer le prix de l’actif sous-jacent en cas de baisse d :
S_d=S_O×d=60×0,9=54
Donc la valeur de C_d est de :
C_d=MAX[0,S-K]=MAX[0,54-62]=0
Sous forme d’arbre, nous obtenons :
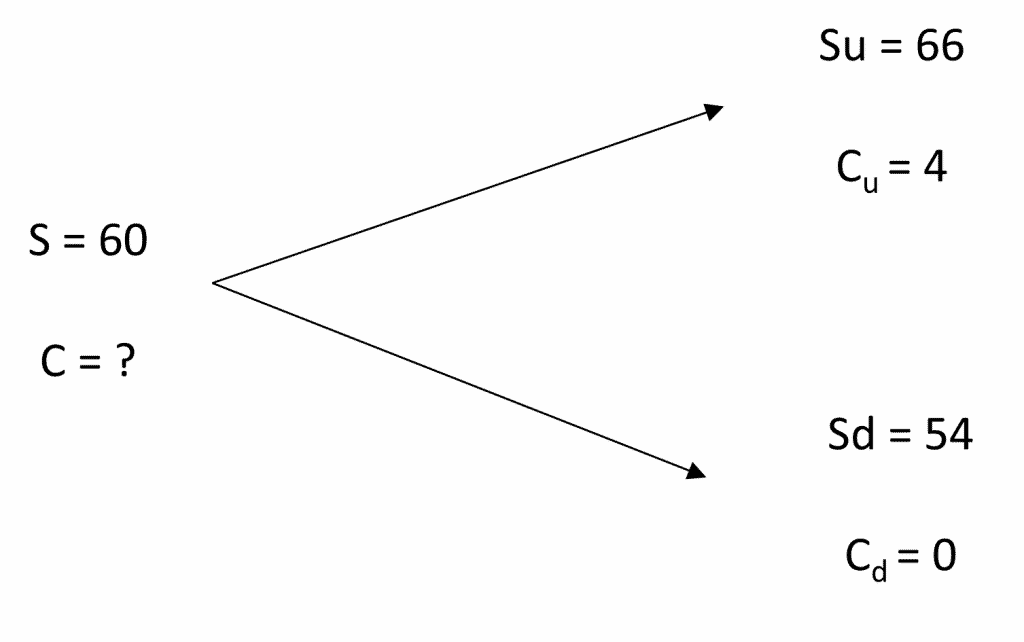
Ainsi la valeur de l’option européenne C est de : C=[p× C_u+(1-p)×C_d ] e^(-rT)
Équivaut à : C=[0,6138×4+(1-0,6138×0] e^(-0,09×0,25)
Équivaut à : C=2,40
4. La méthode Black and Scholes d’évaluation des options
Le modèle de Black-Scholes d’évaluation d’option est l’un des modèles le plus utilisés en mathématiques financières dans le but d’estimer la valeur d’une option. Les travaux de Fischer Black et Myron Scholes, publiés en 1973, constituaient le prolongement des travaux réalisés par Paul Samuelson et Robert Merton. Leur article permet aujourd’hui de déterminer théoriquement la prime exacte que doit payer un trader ou un investisseur pour acquérir un call ou un put, et la stratégie que devra suivre le vendeur de ces options pour se couvrir du risque.
Ce n’est qu’en 1997 que Merton et Scholes se voient finalement récompensés par le prix Nobel d’économie. Black, décédé en 1995, ne pouvait être éligible.
Hypothèse du modèle
Avant de décrire le modèle, il est important de rappeler les hypothèses de ce dernier :
- Le prix de l’actif sous-jacent St suit un mouvement brownien géométrique avec une volatilité σ constante et une dérivée μ constante :
dS_t=μS_t dt+σS_t dW_t où W_t est un processus de Wiener
- Il n’y a pas d’opportunités d’arbitrage ;
- Le temps est une fonction continue ;
- Il est envisageable d’effectuer des ventes à découvert ;
- Il n’y a pas de coûts de transactions ;
- Il existe un taux d’intérêt sans risque, connu à l’avance et constant ;
- Tous les sous-jacents sont idéalement divisibles (on peut par exemple acheter 1/100e d’action) ;
- Dans le cas d’une action, celle-ci ne paie pas de dividendes entre le moment de l’évaluation de l’option et l’échéance de celle-ci.
Formule de Black and Scholes
La formule de Black and Scholes se calcule à partir de plusieurs variables :
- Le prix de l’actif (S) ;
- Le prix d’exercice (K) ;
- La volatilité annualisée (𝜎) ;
- La maturité (T) :
- Le taux d’intérêt sans risque (r).
Avant de développer cette sous-partie, il est important de définir la relation « parité call-put ». Cette dernière évalue la relation entre le prix de vente et le prix d’achat d’une option européenne ayant les mêmes caractéristiques : même prix d’exercice, même sous-jacent et même date d’échéance. Mathématiquement, elle s’écrit :
Put+Sous-jacent=Call+Prix d^’ exercice×e^(-rt)
La parité call-put fait référence à une condition d’équilibre élémentaire entre le prix d’un call et le prix d’un put, tous deux de type européen, et dotés d’une même échéance et d’un prix d’exercice égal.
Ainsi pour une option d’achat et à partir de la relation parité call-put, nous avons :
Call=SN(d_1 )-Ke^(-rt) N(d_2) – Source : www.financedemarche.fr
Pour une option de vente et à partir de la relation parité call-put, nous avons :
Put=Ke^(-rt) N(-d_2 )-SN(-d_1 ) – Source www.financedemarche.fr
Où
d_1=(ln(S/K)+(r+σ^2/2)T)/(σ√T)
Exemple appliqué à la finance
Maintenant que nous avons décrit et posé le modèle, nous pouvons l’appliquer à l’évaluation d’un call européen par exemple.
Soit un call sur une action X. L’action vaut 80 euros à l’instant T. Le prix d’exercice de ce call est de 90 et de maturité un trimestre. Les taux d’intérêt sans risque pour cette période sont équivalents à 5 %. La volatilité implicite est de 35 %.
Donc, nous avons les paramètres ci-après : S = 80, K = 90, T = 0,25, r = 0,05, σ = 0,35.
Nous pouvons calculer d_1 et d_2 :
d_1=(ln(S/K)+(r+σ^2/2)T)/(σ√T)
Équivaut à : d_1=(ln(80/90)+(0,05+〖0,35〗^2/2)0,25)/(0,35√0,25)
Équivaut à : d_1=-0,51
Ainsi : d_2=d_1-σ√T
Équivaut à : d_2=-0,51-0,35√0,25
Équivaut à : d_2=-0,69
Ainsi : 〖N(d〗_1)=0,30 et〖N(d〗_2)=0,25
Par conséquent, nous pouvons déduire le prix du call :
Call=SN(d_1 )-Ke^(-rt) N(d_2)
Équivaut à : Call=80N(d_1 )-90e^(-rt) N(d_2)
Équivaut à : Call=2,48 EUR
Convergence du modèle Cox, Ross et Rubinstein vers le modèle de Black, Scholes et Merton
Dans cette sous-partie, nous allons voir si la convergence des deux modèles est vérifiée.
Pour démontrer cela, prenons l’exemple d’une option d’achat européenne ayant les caractéristiques suivantes :
- Prix de l’actif sous-jacent : 35 ;
- Prix d’exercice de l’option : 36 ;
- Taux d’intérêt sans risque : 5 % (annuel) ;
- Volatilité : 30 % (annuelle) ;
- Maturité : 1 an.
Avec le modèle de Black-Scholes-Merton, le prix d’une telle option est de 4,5169 €.
Quelle est la valeur de cette option avec le modèle de Cox, Ross et Rubinstein ?
Considérons d’abord le cas à une période. Nous pouvons ainsi calculer :
u= e^(σ√T)=1,35
d= e^(-σ√T)=0,74
p=(e^rT-d)/(u-d)=0,51
Ainsi, le prix de cette option d’achat est de :
C=[p× C_u+(1-p)×C_d ] e^(-rT)=5,45
Sous forme d’arbre, nous avons :
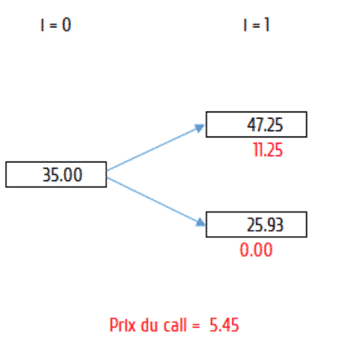
Maintenant, considérons le cas à deux périodes :
u= e^(σ√(T/2))=1,24
d= e^(-σ√(T/2))=0,81
Il vient que : p=(e^rT-d)/(u-d)=0,51
Ainsi, le prix de cette option d’achat est de :
C=[p^2×C_uu +p×(1-p)×C_ud+(1-p)×p×C_du+ 〖(1-p)〗^2×C_dd ] e^(-rT)=4,27
Sous forme d’arbre, nous avons :
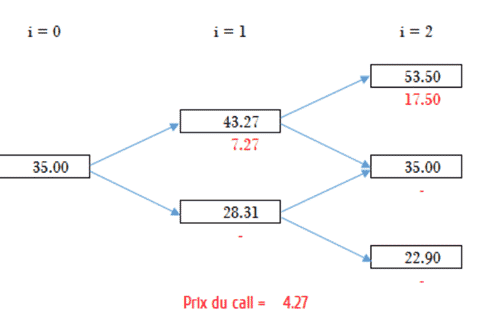
Maintenant, si on pose que T (soit le nombre de périodes) tend vers l’infini, la valeur d’une option calculée à la manière de Cox, Ross et Rubinstein (dans le cas d’un put ou d’un call) donnera, avec les mêmes paramètres, la valeur obtenue avec le modèle de Black and Scholes et Merton :
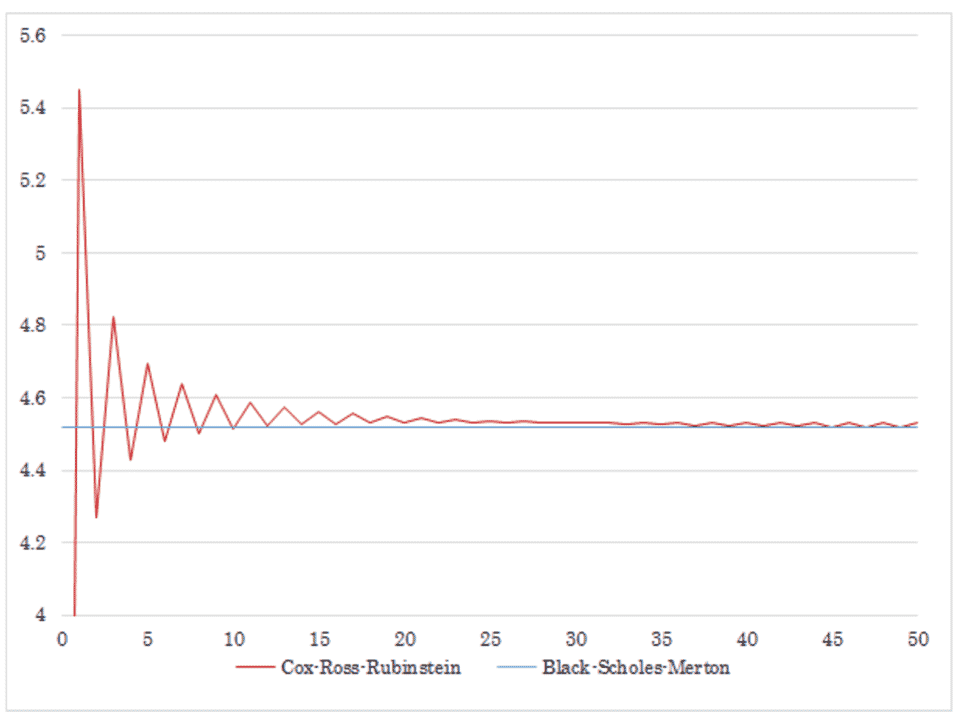
Conclusion
Tout au long de cet article, nous avons essayé de présenter les principaux concepts, méthodes et approches permettant d’évaluer les options. Nous avons vu que ces derniers dépendaient d’un certain nombre de variables. Le modèle proposé par Black et Scholes est le premier et le plus utilisé dans le monde de la finance. L’avantage d’un tel modèle est qu’il permet de trouver la solution exacte pour les prix des options.
Le modèle binomial développé par Cox, Ross et Rubinstein présente l’avantage de s’appliquer sans difficultés particulières à l’évaluation des options européennes et américaines, avec et sans les dividendes. Cependant, l’inconvénient de cette approche est qu’elle nécessite un temps de calcul relativement long pour déterminer le prix d’une option.
Sources
- http://financedemarche.fr/finance/le-modele-de-black-scholes-pour-levaluation-dune-option-avec-un-exemple-numerique
- https://medium.com/magnimetrics/black-scholes-model-first-steps-bdcbe1691da7
- https://www.techno-science.net/definition/6256.html
- https://corporatefinanceinstitute.com/resources/knowledge/valuation/option-pricing-models/
- https://www.fimarkets.com/pages/pricing_grecs.php
- https://d1n7iqsz6ob2ad.cloudfront.net/document/pdf/534d271df2679.pdf
- https://fr.wikipedia.org/wiki/Mod%C3%A8le_binomial
- http://financedemarche.fr/finance/comment-calculer-le-prix-dune-option-a-partir-dun-arbre-binomial-simple-exemple-numerique
- http://www.strategies-options.com/fic/74-le-modele-binomial-une-version-simple-pour-les-options-europeennes.html
- https://mpra.ub.uni-muenchen.de/95486/1/MPRA_paper_95486.pdf
- https://www.lafinancepourtous.com/decryptages/marches-financiers/produits-financiers/options-2/qu-est-ce-que-c-est/la-valeur-d-une-option/
- https://edelit.wordpress.com/2018/03/06/fiche-3-le-principe-darbitrage/
- https://www.amf-france.org/fr/espace-epargnants/comprendre-les-produits-financiers/produits-complexes/options
- https://www.boursedescredits.com/lexique-definition-methode-evaluation-options-2910.php
- https://www.vuibert.fr/system/files/ressources/9782311401745-les-options.pdf
- http://gestion.coursgratuits.net/economie/modele-d-evaluation-des-options-de-black-et-scholes.php
- http://www.fifrance.com/modele_black-scholes.php
- https://fr.wikipedia.org/wiki/Mod%C3%A8le_Black-Scholes
- https://www.boursedescredits.com/lexique-definition-put-call-parity-3832.php
- http://financedemarche.fr/definition/option-americaine
- https://www.mataf.net/fr/edu/glossaire/duree-de-vie-d-une-option
- http://www.iotafinance.com/Article-Les-Strategies-d-Options-1.html
- https://www.net-investissement.fr/placement/guides/fonds-financiers/finance-quest-ce-que-la-volatilite-2318.html
- https://www.ephiquant.com/pricing-des-options-avec-le-modele-de-cox-ross-rubinstein-en-c/




Pas encore de commentaires