Battledev. Post-mortem

Qu’est-ce que la BattleDev ?

C’est une épreuve biannuelle de programmation. Il s’agit de résoudre des problèmes algorithmiques comme dans les autres compétitions de ce type : ACM, Google Code Jam etc. Cependant, la BattleDev est un peu particulière par le fait relativement sympa que :

• La durée est limitée à 2 heures.
• Il faut résoudre 6 problèmes.
• Il faut résoudre un problème pour passer au problème suivant.
• Les niveaux de difficulté montent rapidement : si le 1^er problème est résolu par tous les participants, seule une quinzaine de personnes arrive à résoudre le 6^ème.
• Les méthodes de solution des problèmes ne changent pas entre les saisons. Par exemple, le 5^ème problème concerne la programmation dynamique.

Cette fois, votre humble serviteur a réussi à résoudre 5 problèmes sur 6. Dans cet article, j’aimerais bien ne pas seulement présenter les solutions, mais aussi discuter de la façon avec laquelle on peut arriver à trouver les solutions pour les problèmes algorithmiques en si peu de temps.

Les idées générales

• Écrire un mauvais code. En moyenne, vous avez 20 minutes par problème. C’est le temps de vie exacte de votre code. Après que le problème est validé, il ne sera jamais réutilisé.
• Il n’y a aucune raison d’appliquer les principes de POO. Le développement de classes ou (pire !) de leur hiérarchie est une perte du temps.
• Au lieu de choisir des noms de variables « parlants », préférez les noms courts. Si quelque chose est déjà nommé dans l’énoncé, gardez ce nom. Par exemple, une formule s = a * t * t / 2 est aussi claire que distance = acceleration * movingTime * movingTime / 2.
• Travaillez dans votre IDE préféré. Le site d’épreuve vous fournit une IDE en ligne minimaliste. Mais savez-vous comment utiliser un debuggeur ? Est-ce que tous les raccourcis du clavier sont au bout des vos doigts ? La réponse est « non » pour l’IDE fournie par les organisateurs.
• Avoir un modèle de code avec la lecture d’entrée, car chaque solution doit lire l’entrée de la même façon (voir exemple ci-dessous). Si vous avez accès au système avant la compétition, ce modèle est facile à créer. De plus, on devrait aussi tester le système avant la compétition pour être plus à l’aise pendant.

lines = []

with open('input1.txt') as input_file:
    for line in input_file:
        lines.append(line.rstrip('n'))

# write your solution below...

Exercices 1 et 2 : Échauffement

Pas grand chose à dire. Si vous n’arrivez pas à résoudre l’un des deux exercices au bout de quelques minutes, lisez attentivement le message d’erreur et vérifiez que votre programme « passe » correctement l’entrée et affiche le résultat dans le format demandé. Si les problèmes persistent, relisez l’énoncé et vérifiez que vous avez tout compris. Répétez jusqu’à ce que cela fonctionne.

Exercice 3 : Premier obstacle

Assez gentil, il vous laisse passer sans perte de temps si vous le respectez. Cette année, le problème était le suivant :

Énoncé

Vous êtes dans un champ rectangulaire sur lequel il y a objets de deux classes. Il faut d’abord collecter tous les objets de la première classe, et ensuite, tous les objets de la deuxième classe. La sortie est le parcours nécessaire sous une forme de chaîne de caractères "<", ">", "v", "^". Il n’est pas obligatoire de trouver le parcours optimal.

Idée de la solution

Littéralement, faites ce qu’il est demandé de la façon la plus simple possible :

• Créer une liste de parcours qui contient d’abord les coordonnées des objets de la classe 1, puis celles des objets de la classe 2.
• Écrire une fonction qui trouve un chemin d’un point à l’autre. Testez-la !
• Mettre tout ensemble.

Le plus important ici est de ne pas chercher les complexités : par exemple, le chemin entre deux cases peut être n’importe lequel, mais on choisira un segment horizontal qui est précédé par un segment vertical…

Solution : github

Dirty hack ?

Combien de temps peut-on consacrer à chercher une solution plus rapide si on sait que l’on peut programmer une solution qui marche en temps ? Les mathématiciens répondent par : . Sachant qu’une solution peut être codée en 5-10 minutes, il n’y a pas de raison de chercher des astuces complexes. Cependant, si au bout de 10 minutes, vous avez encore des problèmes, probablement, vous devriez commencer à réfléchir. Ou simplement appliquer les astuces de base…

Exercice 4 : May the brute force be with you

Ce problème peut se transformer en cauchemar, surtout si vous essayez de le résoudre comme dans votre travail (cette semaine, votre humble serviteur a passé 2 jours pour comprendre comment fonctionne un « super-custom-dictionary that caches information about what is loaded and what is proceeded » qui est littéralement une simple couche supplémentaire, mais sophistiquée, autour d’une paire de dictionnaires… Ne le faites pas comme ça !)

Énoncé

Étant donné chaînes de caractères de longueur 10 qui ne contiennent que les 26 lettres de l’alphabet latin, trouvez leur sous-séquence la plus longue. S’il y en a plusieurs, rendez n’importe laquelle. S’il n’y en a aucune, imprimez « KO ».

Le vrai énoncé est un peu plus long : voici une version anglaise, mais j’espère que si vous êtes arrivé au problème 4, alors vous êtes capable de le traduire en langage informatique.

Idée de la solution

Tout d’abord, assurez-vous que vous comprenez ce qu’est une sous-séquence d’une chaîne de caractères. Par exemple, pour une chaîne "abcde", les chaînes suivantes sont les sous-séquences "d", "ace" et "bcd". Mais "f" et "da" ne le sont pas.

De plus, l’énoncé indique explicitement qu’un parcours exhaustif est suffisant pour résoudre le problème, c’est-à-dire qu’il est suffisant de tester toutes les sous-séquences raisonnables. Donc, prenons le mot le plus court, car il en contient moins… Oups, toutes les longueurs des mots sont les mêmes, donc, prenons le premier mot. L’algorithme suivant résout le problème :

max_length = 0
best_subsequence = ''
pour toute sous séquence s du premier mot:
    si s est inclus dans chaque des mots:
        si length(s) < max_length:
            max_length = length(s)
            best_subsequence = s
return best_subsequence

Où peut-on perdre du temps ?

Il y a la tentation de tester d’abord toutes les sous-séquences de longueur 1, puis de longueur 2 et ce, jusqu’à 10. S’il n’y a pas une sous-séquence commune de longueur , alors rendez la sous-séquence commune de longueur . Est-ce que parcourir les sous-séquences de longueur est plus simple que toutes les sous-séquences de toutes les longueurs ?…

À mon avis, le problème 4 est simple et « straightforward », mais il mérite une dizaine de minutes de réflexion pour ne pas choisir un chemin qui cache trop d’obstacles.

Comment tester rapidement toutes les sous-séquences d’un mot ? Chaque sous-séquence correspond naturellement à un nombre binaire dont voici un exemple :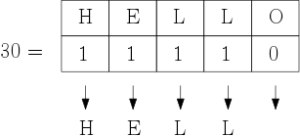

Donc pour tout i = 1..1023 (c’est un nombre de sous-séquences non vides d’un mot de 10 lettres), on calcule la représentation binaire (en python, il y a une fonction standard bin() qui le fait pour vous – n’hésitez pas à chercher sur Internet) de i, puis on génère une sous-séquence (voir le code ci-dessus).

Voici mon code complet. Il est exactement le même que celui que j’ai envoyé pendant l’épreuve. Du point de vue du style, ce n’est sans doute pas ce que j’ai fait de mieux et pour tout vous dire, j’aurais certainement honte de le montrer à un collègue à l’heure actuelle. Cependant, il réalise l’objectif du problème et s’écrit vite. Les lignes commentées sont les traces de tests : je pourrais créer des tests unitaires, mais je n’ai pas envie, car tester mon code sur place est plus rapide dans le cadre d’une compétition de programmation.

Dirty hack ?

Pour moi, l’utilisation d’une fonction bin() en python est déjà un hack — mais propre, car c’est juste une connaissance de la librairie standard.

Mais il existe un vrai « dirty hack » : si on choisit une sous-séquence de s1 au hasard (uniformément, bien sûr), quelle est la probabilité qu’on tombe sur la plus longue sous-séquence commune ? Au mieux, . Mais si on teste sous-séquences aléatoires, la probabilité de ne pas trouver la plus longue sous-séquence commune est
% ! De plus, la librairie standard de python est capable de choisir une sous-séquence aléatoire par une fonction random.sample(sequence, length), dont 10 000 appels prennent moins qu’une seconde.
Voici le code.

Problème 5 : Programmation dynamique

Compliquée à résoudre, mais si vous avez appliqué les conseils de base, il vous reste au moins une heure. Bienvenue dans le monde adulte des concours de la programmation !
Traditionnellement pour la BattleDev, la clé pour le cinquième problème est la programmation dynamique. Comme c’est assez basique, je suppose que vous connaissez le principe.

Énoncé

On est placé dans l’une des cellules d’un couloir 1 x n. La cellule initiale est vide. Dans chacune des autres cellules, il y a soit une pièce valant 1, soit un multiplicateur qui double le profit courant. Si on passe une première fois par une cellule, on collecte l’objet qu’elle contient. L’objectif est de maximiser le profit.
Entrée : cases de couloir, par exemple, dans '*o*X**o' : 'o' = pièce, '*' = multiplicateur, 'X' = position initiale.
Sortie : l’ordre de collecte des objets, par exemple, '*o**o*' qui correspond au profit maximal égal à 10 dans l’exemple ci-dessus.

Idée de la solution

Programmation dynamique ou récursion avec un cache. Soit p[l][r] le profit maximal dans une partie avec un couloir comme sur l’image :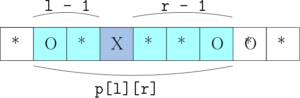

Les instances de bases :

1. car il n’y a qu’une seule case qui est vide.
2. – on est sur le côté gauche d’un couloir, donc il n’y a qu’un ordre possible pour collecter les objets .
3. idem :

Relation récursive :

Comment y arriver

1. Historiquement, le problème numéro 5 se résout avec la programmation dynamique => chercher une récurrence.
2. Parcours optimal sur la « carte » (même 1-D) => chercher une récurrence.
3. Paramétrisation naturelle – la taille du couloir. On peut se prolonger à gauche et à droite indépendamment, on a alors deux paramètres.
4. Récursion ou programmation dynamique ? Si on garde la récursion, chaque appel à solve(l, r) fait appels récursifs à solve(l - 1, ...). Les appels se multiplient comme des lapins en Australie et explose la stack rapidement. Il n’y a pas de choix — la programmation dynamique garde une complexité et taille de stack .

Dirty hack ?

L’algorithme récursif s’écrit très naturellement par rapport à sa version dynamique. Battons le « stack overflow » ! Initialisons le tableau p[l][r] par les -1 et gardons-le comme une variable globale. Nous avons déjà calculé une fois une case de tableau qui a été mise à jour. Donc :

• on sait quelles cases sont déjà calculées, donc on ne les calcule qu’une seule fois ;
• on n’est pas obligé de choisir l’ordre de passage.

Cette méthode s’appelle Récursion avec cache. Le code s’organise de façon suivante :

def solve(l, r):
    if p[l][r] >= 0:  # check if already calculated
        return p[l][r]
    
    result = ...  # usual recursive code

    p[l][r] = result  # save the result in cache
    return result

Voici la solution itérative.
Voici la solution récursive.
Attention ! Malheureusement, on ne peut pas remplacer la programmation dynamique par la récursion avec cache. La raison : les limites de la stack. Clément Carreau a discuté de ce sujet dans son article La récursion terminale à la rescousse ! Dans les concours de programmation, on doit décider vite : est-ce que la solution récursive est faisable ? Pour cela, on peut se référer à une profondeur de stack max de . Ici, , donc la taille de tableau p est limitée à 2500 (pourriez-vous le prouver ?) ainsi que la profondeur de la stack.

Où j’ai perdu du temps

La récurrence est naturelle, mais entre programmation dynamique et récurrence avec cache, j’ai choisi la première. Le résultat ? Une trentaine de minutes face-à-face avec un débuggeur à cause d’un passage incorrect de tableau… La morale est simple : il est important de comprendre quelle solution satisfait les limites avant de l’implémenter.

Problème 6 : La cerise sur le gâteau, mais il ne reste que 1 min 30 s

Énoncé

On donne 2 chaînes de caractères de longueur qui ne contiennent que les 26 lettres de l’alphabet latin. Quand Pierre a tapé ces chaînes, il a perdu certaines lettres consécutives au début et à la fin de chaque chaîne. Après, il a trouvé que les deux chaînes de résultats étaient égales. Quelle est la longueur maximale d’une chaîne que Pierre a rentrée ?

Idée de la solution

D’abord, il faut comprendre qu’il s’agit de trouver la plus longue sous-chaîne commune entre deux chaînes de caractères s1 et s2 de longueur n <= 50000.
Un algorithme en est suffisant.

• Imaginons : nous avons une fonction find(s1, s2, k) qui trouve une sous-chaîne commune de s1 et s2 de longueur k. On en déduit qu’elle existe en temps . Dans ce cas, on trouve la valeur maximale de k en faisant au plus appels au find par la méthode de dichotomie.
• Pour implémenter la fonction find, on applique un algorithme de Rabin-Karp.

Et voici le code.

Comment y arriver

Si vous êtes arrivé à ce point-ci, le mot clé « plus longue sous-chaîne commune » n’est pas étrange. Probablement, vous vous souvenez que la solution par programmation dynamique est simple et existe.
Premier réflexe : aller sur Wikipedia.
La solution attendue est probablement différente des deux proposées par Wikipedia. D’abord, la taille d’un mot, . En général, dans les concours de programmation, votre programme est limité à 256 Mb de mémoire et à 2 s de temps d’exécution. Une règle empirique dit que ce temps est équivalent à ~10^8 opérations.

Donc un algorithme qui marche en ne passera pas les limites du temps (surtout en Python…). La solution qui utilise un arbre de suffixes, marche en . Mais si la complexité est attendue, il serait logique d’avoir une limite …
La complexité la plus populaire entre et est . Comment peut-on obtenir un logarithme dans notre problème ?
– Tri. Normalement, la complexité d’un tri est . Mais on sait que les mots ne contiennent que des lettres, donc le tri comptage prend .
– Dichotomie. Si on peut résoudre un problème du type « Est-ce que s1 et s2 ont la même sous-chaîne de longueur k » en temps , alors on peut appliquer une méthode de dichotomie pour trouver une valeur optimale de k en .

Comment tester que s1 et s2 ont une sous-chaîne commune de longueur k en temps linéaire ?
s1 contient sous-chaînes. Idem pour s2. La comparaison de deux sous-chaînes nécessite opérations. Donc la complexité de brute force est .
La solution passe par l’algorithme de Rabin-Karp.

Dirty hack ?

Il n’y a pas de hack joli comme pour les exercices 4 et 5. Mais Wikipédia constate qu’il y a une solution en temps linéaire qui utilise l’arbre de suffixe. C’est une structure complexe – et qui n’est pas implémentable au bout d’une heure -, mais personne ne vous interdit de chercher une implémentation sur Internet (ainsi que pour la fonction de hachage roulante)…

Je peux aussi imaginer que quelqu’un a déjà implémenté l’arbre de suffixe pour le plaisir et garde une version opérable chez lui. Dans tous les cas, la solution d’au moins un des participants l’a utilisé.

Ma compétition à moi

J’ai terminé 5 exercices en 1h58. Le champion de cette « saison » a tout résolu en une heure. Quelle est la différence entre nous deux ? D’un côté, je connais tous les algorithmes nécessaires pour résoudre les problèmes, mais de l’autre, je suis juste plus lent : je ne fais pas énormément de compétitions de programmation, j’ai produit des bugs, etc.

Seulement ? Revenons sur le problème 6. Mes pensées ont été les suivantes : je connais une solution avec la programmation dynamique. Elle se programme en 2 minutes, je la lance et je vois que sur le test long (2 mots de 50 000 lettres), le calcul prend quelques minutes. Je réfléchis :
– Wikipédia dit : soit programmation dynamique en , soit arbre de suffixe en .
– Je sais que je ne peux pas implémenter la deuxième rapidement et je ne trouve pas une implémentation simple sur Internet.
– Il me faut juste gagner un facteur d’ordre 10, donc j’optimise…
– Les idées : comme les mots ne contiennent que 26 lettres, passer des mots et pour chaque lettre, avoir une liste des indices où cette lettre apparaît.
– Puis, si je teste une sous-chaîne dans un mot, je sais que dans la deuxième, il suffira de vérifier que les sous-chaînes commencent par la même lettre.
– J’essaie des tactiques similaires et au bout de quarante minutes (soit la durée d’un trajet en train entre Versailles et Saint-Lazare), je n’arrive pas à baisser le temps à moins que 20 secondes.

Puis, j’écris à un ami un peu plus expérimenté (beaucoup plus en fait – il est finaliste de l’ACM ICPC) qui me répond en quelques minutes à peine. Je cite : « Essaie une dichotomie par la taille de réponse avec un hachage de sous-chaînes ». Cela était suffisant pour que je me souvienne de l’algorithme de Rabin-Karp et que je produise la solution que vous avez vue au bout d’une demi-heure…

Résumé

Cette épreuve, ainsi que la programmation sportive, n’est pas une question de magie, mais elle nécessite une certaine façon de réfléchir et beaucoup d’expérience, souvent contre-intuitive pour un développeur classique. Je pense que vous avez entendu parler de tous les concepts que j’ai décrits ici. Le vrai problème est de les trouver en seulement 2 heures. Pour cela, je pense que la question « comment arriver à la solution ? » est plus importante que « quelle est la solution ? » Malheureusement, la deuxième question est posée beaucoup plus souvent.