Évaluation d’options européennes par la simulation de Monte-Carlo

Un des défis majeurs en mathématiques financières consiste à évaluer le prix des actifs financiers et autres produits dérivés. Le modèle de Black-Scholes (1973) fournit une formule analytique pour l’évaluation des options d’achat (calls) et de vente (puts) européennes. Ce modèle repose sur l’idée que les prix des actifs financiers évoluent selon un processus de diffusion géométrique, c’est-à-dire que leur variation suit un mouvement brownien géométrique. Néanmoins, lorsqu’il n’existe pas de formules fermées pour évaluer des actifs financiers, d’autres procédures numériques sont utilisées comme la simulation de Monte-Carlo.

La méthode de Monte-Carlo est une application directe de la loi des grands nombres couplée au théorème limite central qui établit la convergence en loi de la somme d’une suite de variables aléatoires vers la loi normale. Elle permet d’approximer la valeur d’une quantité en générant un grand nombre de quantités aléatoires.

Quel est le principe d’une méthode Monte-Carlo ?

Une façon de calculer π par la méthode de Monte-Carlo repose sur une application de la méthode d’acceptation-rejet permettant de simuler des variables aléatoires qui ne nécessitent de connaître la densité cible f qu’à une constante près.

Le principe : on génère des réalisations suivant une densité alternative g qui domine f et pour laquelle on sait facilement simuler. Puis, on introduit un biais à l’aide d’une procédure acceptant certaines réalisations de g et rejetant les autres, permettant d’obtenir un échantillon suivant la densité cible f.

Simulation de Monte-Carlo : exemple

On peut par exemple utiliser l’intégration numérique du quart du disque unité dont l’aire vaut :

A\ =\ \frac{\pi }{4}

Soit (X_n)_n>1, une suite de variables aléatoires indépendantes et uniformes sur le carré [0,1]² dont l’aire vaut 1. La probabilité que X_i tombe dans le disque unité est de :

\frac{A}{S}=\frac{\pi }{4}

Soit (Y_n)_n>1 , une suite de variables aléatoires de Bernoulli. Pour tout i, Y_i vaut 1 si X_i est dans le disque unité : 4E(Y₀) = π

Par la loi des grands nombres, la moyenne empirique de Y_n ​tend vers l’espérance E(Y₀) :

\lim _{n\rightarrow \infty }\frac{4}{n}\sum _{i=1}^nY_i^{\ }=\ 4E\left(Y_0\right)\ =\ \pi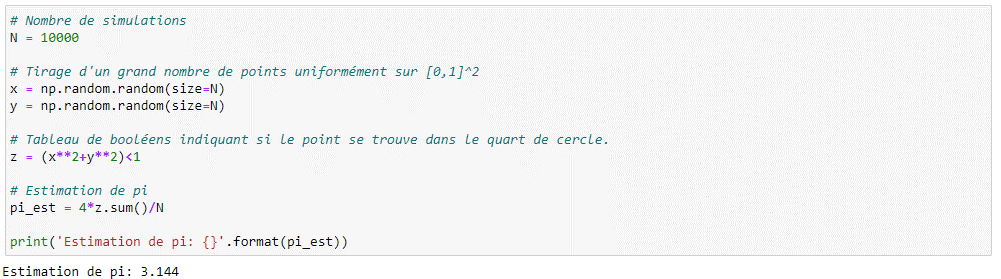 

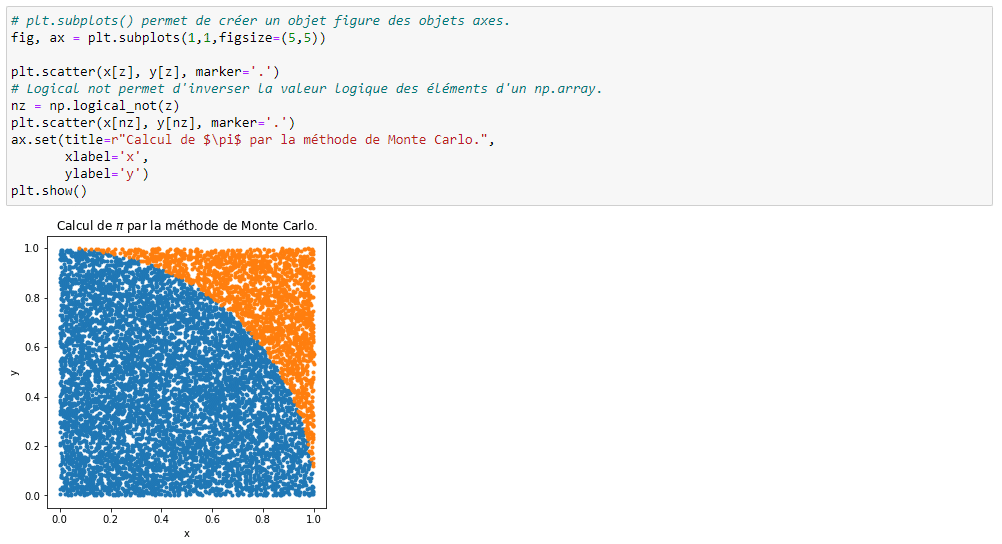
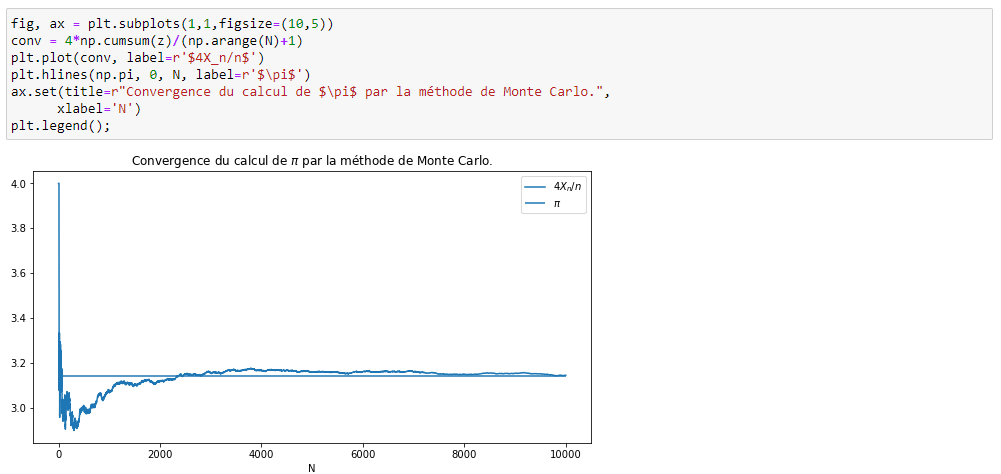
Par l’illustration ci-dessus, on voit ainsi que la moyenne d’un grand nombre d’échantillons d’une variable aléatoire converge lentement vers son espérance.

Comment faire une simulation de Monte-Carlo ?

Comme vu précédemment, les méthodes de Monte-Carlo permettent d’estimer des quantités en utilisant la simulation de variables aléatoires.

Soit l’intégrale :

\int _{A\ }^{\ }g\left(y\right)f\left(y\right)dy\ =\ E\left[g\left(Y\right)\right]

où g est une fonction arbitraire et f une fonction de densité de probabilité telle que :

\int _{\ A}^{\ }f\left(y\right)dy=1

sur le domaine d’intégration A (non mentionné dans les formules).

Description de la méthode et vitesse de convergence

Pour obtenir une approximation de g, on prend un échantillon aléatoire de taille N des valeurs y_i à partir de f, et on calcule ensuite l’estimateur empirique :

g_N^e\ =\ \frac{1}{N}\sum _1^Ng\left(y_i\right)

dont la déviation standard vaut :

\sigma _N^2\ =\ \frac{1}{N-1}\sum _1^N\left(g\left(y_i\right)-g_N^e\right)^2

L’erreur commise par la méthode de Monte-Carlo est aléatoire. Elle ne peut être bornée mais peut être quantifiée via un intervalle de confiance. Sous les hypothèses du théorème limite central, et d’après le théorème de Slutsky, la distribution :

\frac{\left(g_N^e-E\left[g\left(Y\right)\right]\right)}{\sqrt{\frac{\sigma _N^2}{N}}}

tend vers une loi normale centrée réduite. Résultat, l’intervalle de confiance bilatérale symétrique au niveau de confiance asymptotique 1 – α est :

\left[g_N^e-q_{1-\alpha /2}\cdot \sqrt{\frac{\sigma _N^2}{N},}\ g_N^e+q_{1-\alpha /2}\cdot \sqrt{\frac{\sigma _N^2}{N}}\right]

(On prendra usuellement 1−α = 0.95 d’où q1−α/2≈1.96𝑞1−𝛼/2≈1.96)

L’efficacité de la méthode de Monte-Carlo est ainsi évaluée par la largeur de l’intervalle de confiance. Plus précisément, elle relève du facteur :

\frac{\sigma _N}{\sqrt{N}}

qui peut être qualifié de vitesse de convergence.

Elle dépend de deux grandeurs : la variance et le nombre d’itérations. De façon pragmatique, l’augmentation du nombre d’itérations peut souvent s’avérer coûteuse et nécessite des temps de calcul importants, d’où l’intérêt des techniques dites de réduction de variance.

Techniques de réduction de variance

Réduire la déviation standard se fait donc, soit en augmentant le nombre de simulations, ce qui peut être coûteux opérationnellement, soit en réduisant la variance. Dans le cas de cette deuxième option, on parlera de techniques de réduction de variance. L’idée générale est de donner une autre représentation de la quantité à approcher, E[g(Y)], sous la forme d’une espérance E[Z] où Z est une autre variable aléatoire dont la variance est censée être plus petite que celle de σ².

La méthode de la variable de contrôle

Une des techniques est connue comme la méthode de la variable de contrôle de telle sorte que :

Z\ =\ g\left(Y\right)\ -\ X\ +\ E\left[X\right]

On a ainsi :

E\left[g\left(Y\right)\right]=\ G\ +\ \int _{\ }^{\ }g\left(y\right)\left[f\left(y\right)-h\left(y\right)\right]dy

où

G\ =\int _{\ }^{\ }g\left(y\right)h\left(y\right)dy

est calculable.

La méthode de Monte-Carlo

La deuxième partie de l’équation peut aussi être évaluée par la méthode de Monte-Carlo. La densité de probabilité h est la variable de contrôle : l’amélioration de l’efficacité de la méthode repose sur le degré auquel h va imiter le comportement de f sachant que :

var\left(f-h\right)\ \ll \ var\left(f\right)

On obtient donc un nouvel estimateur :

g^c\ =\ G\ +\ \left(g^0-G^0\right)

avec g⁰ et G⁰ deux estimateurs obtenus par Monte-Carlo. La variance du nouvel estimateur vaut :

var\left(g^c\right)\ =\ var\left(g^0\right)+\ var\left(G^0\right)\ -\ 2\cdot cov\left(g^0,G^0\right)

et qui doit être inférieure à celle de g⁰ ce qui donne une condition sur la corrélation entre g⁰ et G⁰ :

corr\left(g^0,G^0\right)\ >\ \frac{1}{2}\sqrt{\frac{var\left(g^0\right)}{var\left(G^0\right)}}

La méthode des variables antithétiques

Alors que cette technique requiert une corrélation positive importante, la méthode dite des variables antithétiques exploite, quant à elle, la corrélation négative entre les estimateurs. L’idée est ici de calculer deux valeurs de l’estimateur en utilisant des symétries du problème :

1. La première valeur de l’estimateur est calculée à partir d’une série de y_i​ générée en utilisant des variables aléatoires u_i tirées uniformément entre 0 et 1.
2. La seconde est déterminée en changeant le signe des tirages aléatoires.

L’estimateur recalculé de E[g(Y)] est donc la moyenne des estimateurs obtenus :

\frac{1}{2}\cdot \left[g\left(u\right)+g\left(1-u\right)\right]

et dont la variance vaut :

\frac{1}{4}\left[var\left(g\left(u\right)\right)+var\left(g\left(1-u\right)\right)\right]+\ \frac{1}{2}\left[cov\left(g\left(u\right),g\left(1-u\right)\right)\right]

Le second terme additif de l’équation capture la covariance entre les estimateurs. Si son signe est positif, la variance du nouvel estimateur sera importante. Mais, si son signe est négatif, la variance en sera réduite, ce qui explique pourquoi on cherchera à avoir une covariance négative entre les estimateurs de base.

L’échantillonnage préférentiel

Une autre technique s’appelle l’échantillonnage préférentiel dont le principe est le suivant : il s’agit d’estimer l’espérance d’une fonction g par rapport à une distribution cible φ en utilisant l’espérance de la même fonction g mais en tenant compte des différences entre les distributions grâce à des poids d’importance basés sur le rapport f / φ par rapport à la distribution cible f.

Cette technique est particulièrement utile lorsque f et φ sont significativement différentes, car elle permet de réduire la variance de l’estimation par rapport à l’approche de base. En attribuant des poids d’importance aux échantillons, elle permet d’obtenir des estimations plus précises de l’espérance de g sous φ, ce qui améliore l’efficacité des simulations de Monte-Carlo dans de telles situations.

Soit φ une autre densité sur A et X une variable aléatoire de densité φ, alors :

E\left[g\left(Y\right)\right]=\int _{\ }^{\ }\frac{g\left(y\right)f\left(y\right)}{\varphi \left(y\right)}\varphi \left(y\right)dy\ =\ E\left[\frac{g\left(X\right)f\left(X\right)}{\varphi \left(X\right)}\right]

Si on note :

Z\ =\frac{g\left(X\right)f\left(X\right)}{\varphi \left(X\right)}

le calcul de l’espérance par l’approximation :

\frac{1}{N}\sum _{i=1}^N\frac{g\left(X_i\right)f\left(X_i\right)}{\varphi \left(X_i\right)}

pour une suite (X_i) indépendante et identiquement distribuée de densité φ sera plus efficace que par l’approximation de base si :

var\left(Z\right)\ \ll \ var\left(g\left(Y\right)\right)

Cette technique est notamment adaptée dans le cas où il n’est pas optimal de générer des variables aléatoires dans les parties de A où la fonction g est nulle ou quasi nulle. On choisit alors une autre loi que f afin d’avoir davantage de réalisations dans les parties où g est non nulle et on pondère ces réalisations pour corriger le changement de loi. Le rapport f / φ sera appelé poids d’importance dans cette technique.

Les autres techniques de réduction de variance

Il existe enfin d’autres techniques de réduction de variance telles que la méthode de stratification ou encore le conditionnement. L’ensemble des techniques présentées ainsi que celles mentionnées sont faciles à mettre en place et visent à améliorer l’efficacité des simulations de Monte-Carlo en réduisant la variabilité des estimations. Ce qui peut se traduire par des estimations plus précises en utilisant un nombre moins élevé de simulations et donc une minimisation du temps de calcul.

💡 Découvrez notre guide sur l’ajustement de stratégie de trading avec les options !
Vous souhaitez optimiser votre portefeuille ? Plongez dans notre article pour tout savoir sur l’évaluation des options avec les méthodes binomiale et de Black and Scholes. Apprenez à maîtriser ces outils incontournables pour affiner vos décisions d’investissement !

Application à la valorisation d’options

Introduite par Boyle (1977) en finance quantitative, la simulation repose en grande partie sur l’évaluation risque-neutre : les paiements futurs espérés sont en effet calculés dans l’univers risque-neutre en suivant une procédure d’échantillonnage, avant d’être actualisés au taux d’intérêt sans risque.

Le calcul du prix d’une option revient à la solution d’une équation différentielle. Or, d’après le théorème de Feynman-Kac, une équation différentielle peut être représentée par une espérance mathématique et donc une intégrale. D’où l’intérêt de la simulation de Monte-Carlo pour la valorisation d’options.

Scénario de simulation de Monte-Carlo

On considère une option ayant pour support une variable de marché S et délivrant un payoff à la date T. On peut donc évaluer cette option de la manière suivante :

1. Tirer au hasard une trajectoire de S.
2. Calculer le flux payé à l’échéance par l’actif dérivé pour cette trajectoire.
3. Répéter les 2 premières étapes de façon à disposer d’un grand nombre de flux terminaux de l’option dans l’univers risque-neutre.
4. Calculer la moyenne des flux.
5. Actualiser le flux terminal espéré au taux d’intérêt sans risque pour avoir la valeur de l’option.

On peut ainsi supposer que la variable sous-jacente suit un mouvement brownien géométrique, ce qui permet de simuler la trajectoire en fonction d’un pas de temps et du nombre de simulations.

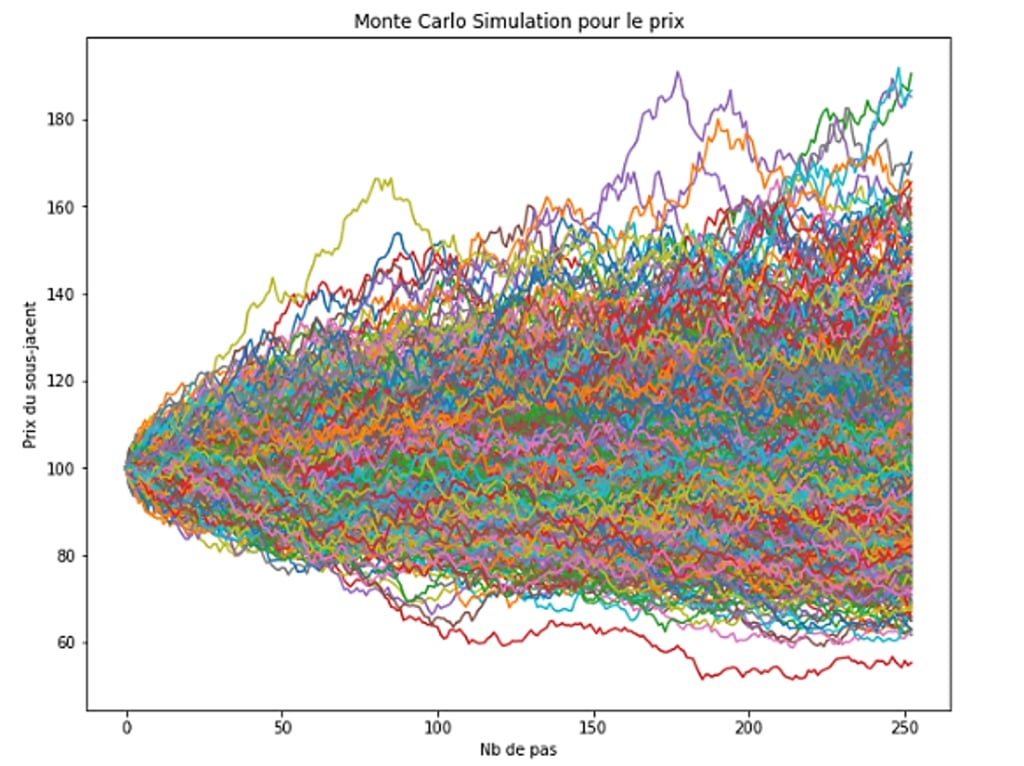
Dans le cas d’une option d’achat (call) européenne, le payoff vaut :

\max \left(S_T-K,\ 0\right)

La formule de Black-Scholes s’applique aussi pour le call et servira de benchmark.

En utilisant de façon naïve la méthode de Monte-Carlo, il est possible d’avoir une approximation proche de la valeur obtenue par Black-Scholes :

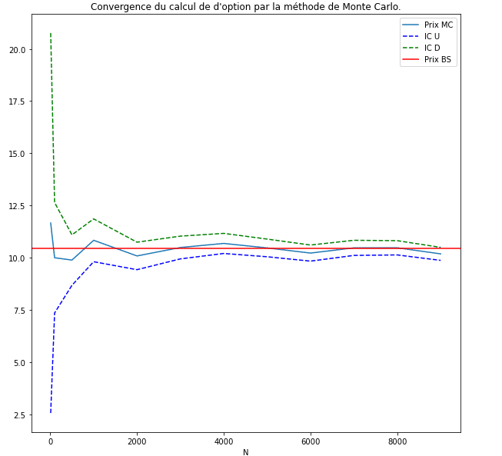
Quelles techniques de réduction de variance utiliser ?

Comme introduites précédemment, différentes techniques de réduction de variance s’appliquent pour le calcul du call européen.

La méthode des variables antithétiques propose en effet des intervalles de confiance plus étroits pour un même nombre de simulations, témoin que la variance a été réduite :

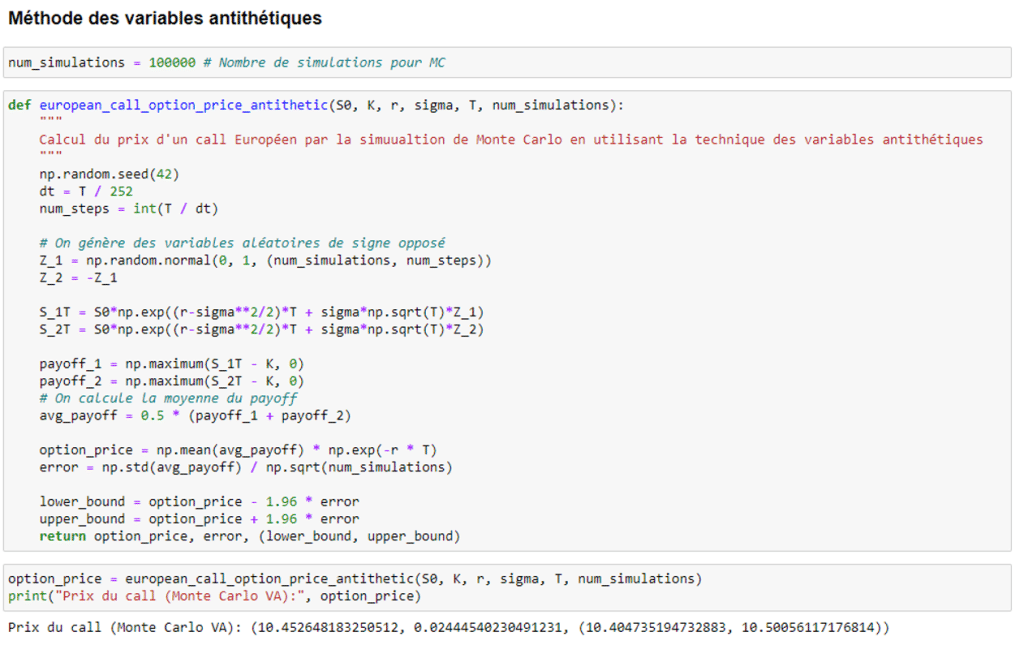
Pour la méthode de la variable de contrôle, il est possible de s’appuyer sur la parité call-put pour utiliser le payoff du put comme variable de contrôle pour réduire la variance :

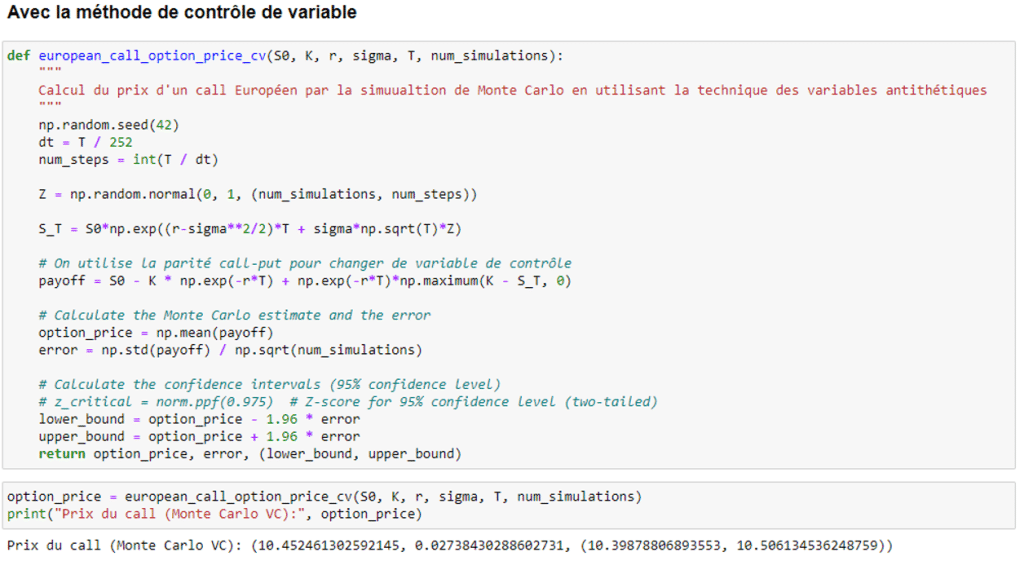
Enfin, pour l’échantillonnage préférentiel, si l’on se place dans un cas où S<<K sont significativement différentes, on peut alors avoir une nette réduction de variance par rapport à la méthode naïve de Monte-Carlo.

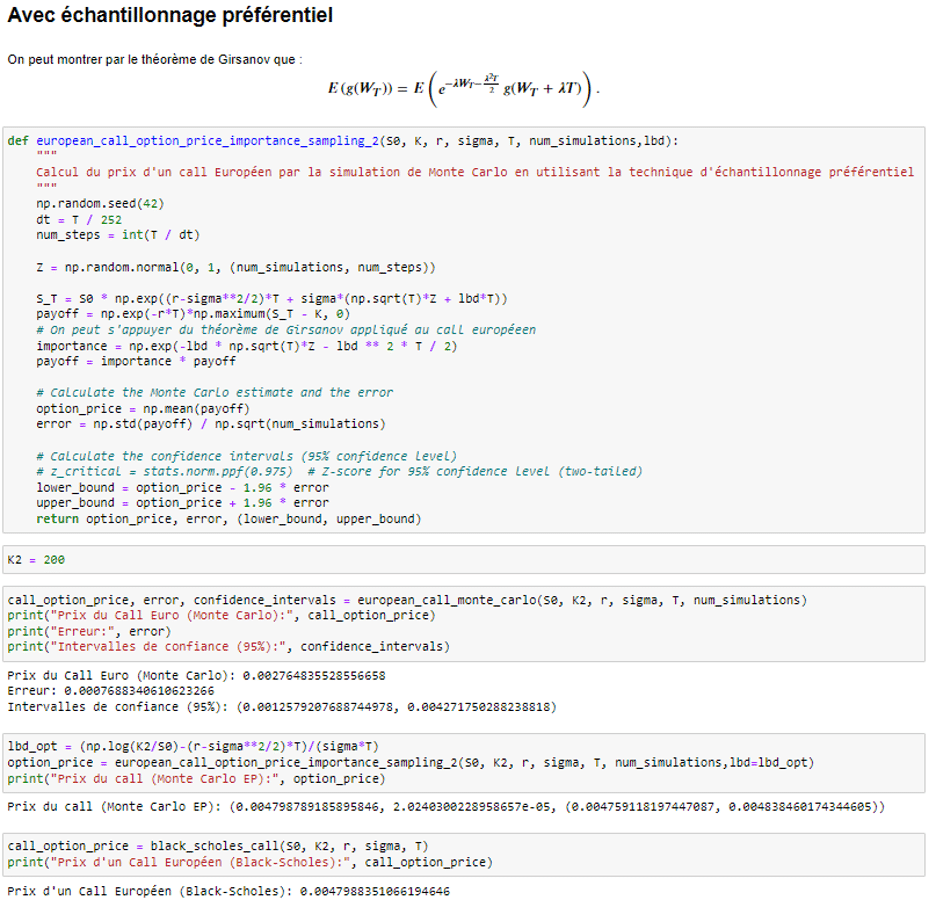
📥 Restez informé en vous abonnant à notre newsletter pour recevoir des articles, des études de cas et des actualités directement dans votre boîte mail.

Conclusion

Si dans les exemples ci-dessus, l’application numérique s’appuie sur des flux à l’échéance T, il est aussi possible de générer de façon discrète les trajectoires de flux par pas de temps. Par exemple, dans l’article de Boyle (1977), un mécanisme de paiement discret de dividendes est introduit à chaque étape de la simulation d’un mouvement de S_t .

Finalement, la méthode de Monte-Carlo s’avère particulièrement utile pour des options plus complexes, telles que des options dont les payoffs dépendent du chemin suivi par S : les options asiatiques, des paniers d’options, ou bien encore lorsque l’on travaille sur des processus avec sauts. Un des avantages notables de la méthode de Monte-Carlo est qu’elle est flexible par rapport à la distribution utilisée pour générer les rendements des sous-jacents.

En guise d’ouverture, il est aussi possible d’utiliser les simulations de Monte-Carlo pour le calcul des grecques. Ce sont des mesures de risque utilisées pour quantifier l’influence des différents paramètres sur le prix d’une option. Or leur calcul est rarement évident et il n’y a pas forcément de formules fermées pour les évaluer. D’où la simulation pour obtenir des bonnes approximations de ces grecques.

Ressources

• Options: A Monte-Carlo Approach – P.Boyle (1977)
• Monte-Carlo Methods and Stochastic Algorithms – B.Lapeyre, B.Jourdain (2022)
• Méthodes de Monte-Carlo pour la finance – E.Temam (2004)
• Méthodes de Monte-Carlo – A.Millet (2006)
• Méthodes de Monte-Carlo – J.Stoehr (2023)
• GitHub Meritis : EuropeanOptionPricing