Les algorithmes génétiques sont des méthodes d’optimisation stochastique basées sur les mécanismes de la sélection naturelle et de l’évolution des espèces. Développés initialement par John Holland, leurs champs d’application sont très vastes…
De nombreuses techniques s’ouvrent aux investisseurs désireux de découvrir de nouvelles méthodes de trading gagnantes. Parmi celles-ci, les algorithmes génétiques, technique simple et efficace qui repose sur les mécanismes de la sélection naturelle et de l’évolution des espèces. Dans cette première partie, nous nous attacherons à présenter et à expliquer leur fonctionnement pour mieux comprendre leur impact.
I/ Présentation des différentes techniques
La stratégie « Buy-and-Hold » consiste à sélectionner des actions soigneusement selon une analyse approfondie de l’entreprise et de son secteur, et à les conserver à long terme, sans essayer de les revendre pour encaisser une plus-value. Cette approche adoptée par les plus grands investisseurs sur les marchés boursiers présente de nombreux avantages, tout en étant relativement simple à mettre en œuvre. De même, elle peut afficher de belles performances lorsqu’elle est bien appliquée.
Cependant, d’autres investisseurs préfèrent utiliser une stratégie active, communément appelée le « Market Timing », c’est-à-dire essayer d’acheter au plus bas et de revendre au plus haut. De multiples options s’ouvrent aux investisseurs. Grâce aux nouvelles technologies, ceux-ci peuvent soit utiliser des méthodes qui s’inspirent de l’intelligence artificielle – telles que les réseaux de neurones, la logique floue et les algorithmes génétiques –, soit employer l’analyse technique.
L’analyse technique
Pratiquée à l’origine par les Japonais au XVIIIe siècle pour prévoir l’évolution des cours du riz, cette méthode est utilisée aujourd’hui par de nombreux investisseurs dans les milieux financiers. Le principe est le suivant : il s’agit d’étudier et d’anticiper les mouvements de cours des marchés financiers, en se basant sur les données historiques d’un actif.
L’analyse technique est essentiellement le reflet de l’idée que les prix fluctuent selon une tendance déterminée par un changement d’attitude des investisseurs à travers une variété de forces économiques, monétaires et politiques.
La lecture d’une courbe des prix d’un actif financier revient à analyser l’évolution de la réaction des investisseurs sur le marché. Ont-ils plutôt acheté ou vendu ? Ont-ils paniqué ? Ou ont-ils été euphoriques ? Pourquoi un acteur a-t-il subitement liquidé ses positions ? Ainsi, le cours d’un actif boursier peut être représenté comme un inconscient collectif retranscrit. L’analyse technique permet alors de le déchiffrer et de l’interpréter.
Par conséquent, puisque l’analyse technique permet de déchiffrer cet inconscient collectif, il serait donc possible de prédire les mouvements des prix futurs et ce, en évoquant l’hypothèse que la psychologie des investisseurs bouge entre la panique, la peur, le pessimisme, la confiance, l’optimisme excessif et l’avidité.
La programmation génétique
Une nouvelle technique qui est encore peu utilisée dans le monde de la finance, mais n’en reste pas moins très prometteuse, est la programmation génétique. Cette nouvelle méthode permet à un investisseur d’identifier, à travers un espace de solutions, une formule mathématique applicable sur les marchés financiers.
Tout comme les algorithmes génétiques, cette méthode d’optimisation s’inspire du processus d’évolution des espèces de Darwin. Il a été établi que la programmation génétique peut être une solution efficace dans de nombreux domaines. Ainsi, certains auteurs ont décidé d’utiliser cette méthode pour résoudre différents problèmes dans le domaine financier.
II/ Les algorithmes génétiques
Les algorithmes génétiques sont des méthodes d’optimisation stochastique basées sur les mécanismes de la sélection naturelle et de l’évolution des espèces. Développés initialement par John Holland, leurs champs d’application sont très vastes. En effet, les algorithmes génétiques peuvent être employés pour la construction de portraits robots, la planification des horaires, les courses de chevaux, le design des avions ou encore en programmation génétique, en théorie du contrôle optimal, etc.
Plusieurs raisons expliquent ce grand nombre d’applications, à commencer par la simplicité et l’efficacité de ces algorithmes. Encore peu utilisés en finance, l’intérêt porté pour ces derniers dans les milieux financiers est toutefois en forte croissance.
La théorie de Darwin
Pour développer les algorithmes génétiques, John Holland s’est inspiré de la théorie de Darwin. Selon cette théorie, les individus (espèces animales et végétales) ont dû évoluer pour survivre, en s’adaptant de génération en génération aux variations de leur environnement, afin de mieux y vivre.
Selon lui, l’évolution se fait par le principe de sélection naturelle : seuls les animaux les plus adaptés à leur milieu survivent. Ce sont donc eux qui auront le plus de chance de se reproduire et de transmettre leurs gènes. Ainsi, un animal qui aurait une anomalie génétique (par exemple : plus de poils que ses congénères) aura plus de chance de survivre dans un environnement plus froid. Il pourra donc transmettre cette « anomalie positive » à toute sa descendance. Cette mutation se diffusera rapidement à toutes les nouvelles générations de cette espèce.
La preuve par l’exemple : le cas des girafes
Pour mieux comprendre, prenons le cas des girafes. Ces dernières se nourrissent principalement de feuilles poussant sur les arbres. Si, sur une génération de girafes, quelques-unes ont un cou plus long, ces dernières ont un avantage par rapport aux autres leur permettant ainsi d’atteindre les feuilles se trouvant plus haut dans les arbres.
Maintenant, si toutes les feuilles en bas ont déjà été mangées, les girafes au petit cou meurent de faim, celles au cou long survivent et peuvent se reproduire. Lors de la prochaine génération, il y aura donc plus de girafes qui auront hérité du « long cou » de leurs parents… Et ceci a continué pendant des millions d’années. En conséquence, cet avantage permet aux girafes de s’adapter au milieu, de vivre plus longtemps et de se reproduire.
Les algorithmes génétiques constituent donc des méthodes d’optimisation stochastique basées sur la sélection naturelle et sur l’évolution des espèces qui consistent à maintenir « en vie » une population composée de chromosomes étant en compétition entre eux. Chaque chromosome représente une solution potentielle au problème que l’utilisateur tente de résoudre. De génération en génération, les chromosomes sont transformés par des opérations inspirées de la biologie. À la fin du processus, les chromosomes les plus performants devraient dominer la population.
III/ Comment fonctionnent les algorithmes génétiques ?
Afin de faciliter la lecture et la compréhension du lecteur, cette section illustre l’exemple d’un investisseur qui souhaite optimiser une moyenne mobile sur une action boursière aléatoire. Une moyenne mobile définit la tendance d’un cours en se basant sur la moyenne de ses performances, ce qui permet d’identifier des positions d’achat ou de vente. En d’autres termes, l’objectif est de se positionner sur un titre avant que la tendance ne se soit totalement exprimée.
Cet indicateur de tendance boursière se calcule en additionnant les X cours de clôture que l’on divise par le nombre total d’observation, donnant ainsi la moyenne du prix sur ces X observations consécutives. Le terme « mobile » vient du fait qu’à chaque nouvelle observation, la moyenne calculée se « déplace » d’une observation pour ne tenir compte que des X derniers.
Ainsi, un titre qui voit son cours passer par-dessus sa moyenne mobile démontre une forte attractivité de la part des investisseurs. Au contraire, une action qui casse sa moyenne mobile sera considérée comme une action en perte de vitesse. Les moyennes mobiles servant alors de supports et de résistances. Dans un tel scénario, l’utilisation des algorithmes génétiques permet à l’investisseur de trouver les X cours qui maximiseront ses gains.
Représentation du problème
Un algorithme génétique implémente une version très simplifiée et très schématique des mécanismes de l’évolution. La première étape de la mise en œuvre d’un algorithme génétique consiste à construire une représentation des solutions potentielles aux problèmes sous forme de chromosomes, c’est-à-dire en code binaire 0 et 1.
Le codage binaire est non seulement la manière la plus simple mais aussi la plus répandue de représenter un chromosome dans un contexte informatique. Les 0 et 1 représentent les gènes contenant les caractéristiques d’une solution. Les chromosomes composant une population sont tous de la même taille et doivent contenir suffisamment de gènes afin que la solution recherchée puisse être représentée.
Par exemple, pour un investisseur souhaitant optimiser une moyenne mobile, les solutions potentielles du problème seront donc représentées par le nombre de jours nécessaires pour le calcul de celle-ci. Ainsi, chaque chromosome va correspondre à un nombre de jours. Par exemple, 000001110 peut être décodé de la manière suivante :
0×2^8+ 0×2^7+0×2^6+0×2^5+0×2^4+0×2^3+0×2^2+0×2^1+0×2^0=14
Dans notre exemple, le chromosome équivaudrait à 14 jours. Ici, l’exemple nécessite l’optimisation d’une seule variable. Cependant, il peut arriver parfois qu’un problème d’optimisation exige plusieurs variables. Dans ce cas, le chromosome sera divisé en plusieurs parties, de façon à ce que chaque partie représente une variable.
Pour résoudre un tel problème, nous allons utiliser une fonction objective. Le terme « fonction objective » est utilisé en optimisation mathématique pour désigner une fonction qui sert de critère pour déterminer la meilleure solution à un problème d’optimisation. Concrètement, elle associe une valeur à une instance d’un problème d’optimisation. Le but du problème d’optimisation est alors de minimiser ou de maximiser cette fonction jusqu’à l’optimum par différents procédés, comme l’algorithme du simplexe.[1]
Création de la population initiale
Pour démarrer un algorithme génétique, il faut lui fournir une population aléatoirement créée et que l’on peut faire évoluer. Une population est un ensemble de chromosomes (aussi appelé individus) représentant chacun une solution potentielle au problème posé. Il n’est nullement besoin de songer à créer de bons individus. Ils doivent juste rentrer dans le « moule » du problème posé.
Par exemple, si le but est de chercher un chemin entre deux points, les individus créés devront simplement posséder le bon point de départ et le bon point d’arrivée, peu importe par où ils passent.
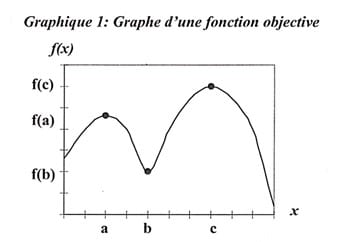
Graphiquement, un optimum local représente un point où la fonction objective est croissante ou décroissante de chaque côté de ce point. Ainsi, cette fonction objective servira de critère pour déterminer la meilleure solution à un problème d’optimisation.
Par exemple, la fonction objective représentée sur le graphique 1 contient un maximum et un minimum respectivement aux points b et c, et un maximum absolu au point c. Ce maximum absolu indique donc qu’il n’existe aucun autre point sur l’axe des abscisses qui pourrait donner une valeur supérieure à la fonction objective.
Mesure de la performance des chromosomes
Une fois que la population initiale a été créée, une mesure de la performance, la fitness, doit être calculée pour chaque individu. Cette étape permet d’identifier les individus les plus prometteurs, c’est-à-dire ceux qui auront le plus de chance de se reproduire lors des générations futures et qui participeront par conséquent à l’amélioration de la population.
Cette étape intermédiaire de mesure de la performance des chromosomes peut même devenir une étape importante du processus d’amélioration de la population. En effet, les différents individus ne sont pas toujours comparables : il n’est pas toujours possible de dire qu’un individu est meilleur ou moins bon qu’un autre. C’est principalement le cas lorsqu’une solution dépend de plusieurs paramètres.
Toujours en considérant l’exemple d’un investisseur souhaitant optimiser le paramètre d’une moyenne mobile, l’excess return (rendement excédentaire) par rapport à une stratégie Buy-and-Hold peut être considéré comme mesure de la performance.
Sélection
Selon Darwin, seuls les individus adaptés à leur environnement survivent. La sélection consiste à choisir les individus les mieux adaptés afin d’avoir une population la plus proche de converger vers l’optimum global. Pour ce faire, l’algorithme génétique élimine les individus médiocres pour les remplacer par ceux qui ont de meilleures mesures de la performance.
L’opération de sélection se divise en deux étapes :
- La première consiste à choisir les individus qui possèdent une mesure de la performance la plus élevée.
- La seconde consiste à transférer ces individus dans une population intermédiaire.
Reproduction
Comme dans tout système biologique, les meilleurs individus de la population initiale sont ceux qui ont une meilleure chance de se reproduire et de transmettre une partie de leurs gènes à la prochaine génération. Ainsi, la reproduction est l’étape la plus importante dans l’élaboration d’un algorithme génétique.
Cette dernière peut se décrire en quatre étapes :
- Premièrement, les parents de la population intermédiaire fusionnent pour former de nouvelles paires de chromosomes.
- Ensuite, pour chacune d’entre elles, il faut déterminer si un croisement est possible via un taux de croisement. Ce taux est habituellement fixé à 60 %. Lorsque le croisement n’est pas possible, les chromosomes parents sont copiés tels quels dans la nouvelle population.
- Troisièmement, lorsque la reproduction est possible, un point de croisement commun est sélectionné aléatoirement selon une loi uniforme.
- Enfin, les parties de chaque chromosome parent sont échangées.
Mutation
Pour créer de nouveaux individus, il est possible de modifier ceux déjà existants. La mutation a l’avantage de conserver une certaine diversité dans la population et réduit les risques de converger rapidement vers un optimum local. La mutation consiste à modifier aléatoirement des individus de la population initiale en en modifiant un gène.
Rien ne nous dit que l’individu muté sera meilleur ou moins bon, mais il apportera des possibilités supplémentaires qui pourraient bien être utiles pour la création de bonnes solutions. Les chances de transformation seront déterminées selon un taux de mutation fixé par l’utilisateur. Ce taux est généralement très petit, habituellement fixé à 1 %. Cependant, il est bon de noter qu’un taux trop élevé rendrait inutile l’étape de sélection.
Critères d’arrêt
L’algorithme génétique s’arrête une fois que les critères d’arrêts fixés par l’utilisateur sont satisfaits. Si tel est le cas, alors la solution finale est l’individu généré qui possède la meilleure mesure de la performance. Sinon, l’utilisateur devra répéter les différentes étapes de sélection. Habituellement, les critères d’arrêt choisis par l’utilisateur sont le degré d’homogénéité de la population, le plateau évolutif et le nombre fixe de génération.
Conclusion
La première étape de la mise en œuvre d’un algorithme génétique consiste à construire une représentation des solutions potentielles aux problèmes sous forme de chromosomes. Par la suite, une population initiale est créée. Après avoir associé à chaque chromosome une mesure de la performance, les opérations de sélection, de reproduction et de mutation sont réalisées selon les paramètres de l’utilisateur afin de créer une nouvelle population. Ces opérations sont répétées jusqu’à ce qu’un critère d’arrêt, fixé par l’utilisateur, soit satisfait. Lorsque le processus d’optimisation est terminé, la solution finale correspond à l’individu qui possède la mesure de la performance la plus élevée.
Dans le prochain article, nous verrons si réellement le programme des algorithmes génétiques modifie les méthodes de trading actuelles.
Sources
- https://www.researchgate.net/publication/5085159_Presentation_des_algorithmes_genetiques_et_de_leurs_applications_en_economie
- https://fr.wikipedia.org/wiki/Fonction_objectif
- https://khayyam.developpez.com/articles/algo/genetic/
- Maxime Vallée, “L’utilisation de la programmation génétique pour découvrir des règles d’analyse technique », Travail dirigé, M.Sc., Ecole des Hautes Etudes Commerciales, Montréal, Canada.
- Thomas Vallée, Murat Yildizoğlu, “Présentation des algorithmes génétiques et de leurs applications en économie “, Revue d’économie politique, Vol. 114, No. 6 (novembre-décembre 2004), pp. 711-745.
- Brock W.; Lakonishok J.; LeBaron B., (1992), “Simple Technical Trading Rules and the Stochastic Properties of Stock Returns”, Journal of Finance, volume 47, p. 1731-1764.
- Bourrassé T., (1996), Application d’un algorithme génétique à la recherche des caractéristiques gagnantes des actions boursières canadiennes, Travail dirigé, M.Sc., Ecole des Hautes Etudes Commerciales, Montréal, Canada.
[1] https://fr.wikipedia.org/wiki/Fonction_objectif



Pas encore de commentaires