Le Compact Prediction Tree (CPT), qu’est-ce que c’est ? C’est un algorithme “spécifique” qui propose une nouvelle approche dite “sans perte” et s’articule autour de trois structures de données. Retrouvez dans cet article tout ce que vous avez toujours voulu savoir (ou devez savoir) sur le CPT.
La prédiction de séquence sur un alphabet fini ? Kézako ?
La prédiction de séquence est un problème d’apprentissage automatique supervisé, ici nous nous attardons particulièrement sur la prédiction d’un élément d’un ensemble de taille finie survenant après une séquence ordonnée donnée.
Par exemple, suite à cette séquence : [0, 1, 2, 3, 4], nous aimerions que notre algorithme prédise 5.
Ce problème, longuement étudié, connaît plusieurs domaines d’applications. On pense notamment au préchargement de contenus web (pages, vidéos, etc.), à la recommandation de produit ou encore à la compression de fichier adaptative. Dans la compression adaptive, la prédiction est utilisée pour encoder les caractères restants les plus probables avec le moins de bits possibles. La prédiction dans le préchargement de contenu quant à elle est utilisée pour améliorer l’expérience utilisateur en réduisant le temps d’attente.
Pour résoudre cette catégorie de problèmes, nous pouvons adapter des algorithmes “classiques” de type ensemblistes ou réseaux de neurones. Mais il existe également des algorithmes plus spécifiques, parmi lesquels le “Prediction by Partial Matching”, le “Dependency Graph” ou encore le “Compact Prediction Tree” que nous allons étudier ici.
Le Compact Prediction Tree (CPT) tente une nouvelle approche grâce à un modèle dit “sans perte”, c’est-à-dire qu’il ne perd aucune donnée lors de l’entraînement de son modèle. Il est capable de restituer les séquences d’entraînement après entraînement. Ce n’est pas le cas des algorithmes tels que le Random Forest où nous ne pouvons retrouver qu’un agrégat de données au travers des arbres. Cette nouvelle approche permettrait ainsi d’avoir une meilleure précision lors des prédictions.
C’est en 2013 que l’idée du Compact Prediction Tree a été publiée officiellement par l’équipe du département Informatique de l’université de Moncton. En 2015, ces mêmes auteurs nous proposent une version améliorée : le CPT+ (meilleure gestion du bruit et réduction de l’empreinte mémoire).
Dans cet article, je vais détailler la manière dont le CPT s’entraîne, prédit et avec quelles structures de données. Je vous montrerai ensuite comment entraîner un modèle CPT en quelques lignes de code.
Introduction de l’algorithme CPT
Le modèle CPT s’articule autour de trois structures de données permettant la compression de toutes les séquences d’entraînement, un accès en temps constant aux séquences d’entraînement et un entraînement en temps linéaire par rapport au nombre de séquences.
Voici donc une présentation succincte de ces trois structures de données.
Arbre de prédiction
Le modèle CPT utilise un arbre de prédiction qui n’est rien d’autre qu’un arbre préfixe, également appelé tree en anglais. Les arbres préfixes sont une structure de données basée sur un arbre permettant de stocker des séquences. Ils sont utilisés dans des algorithmes tels que l’auto-complétion des mots. Ils servent à diminuer la complexité de prédiction, par rapport à l’utilisation de listes.
Par exemple, si on compresse les séquences de lettres suivantes : “mot”, “mo”, “mois”, “omit” et “pos”, nous aboutissons à l’arbre de prédiction ci-dessous :
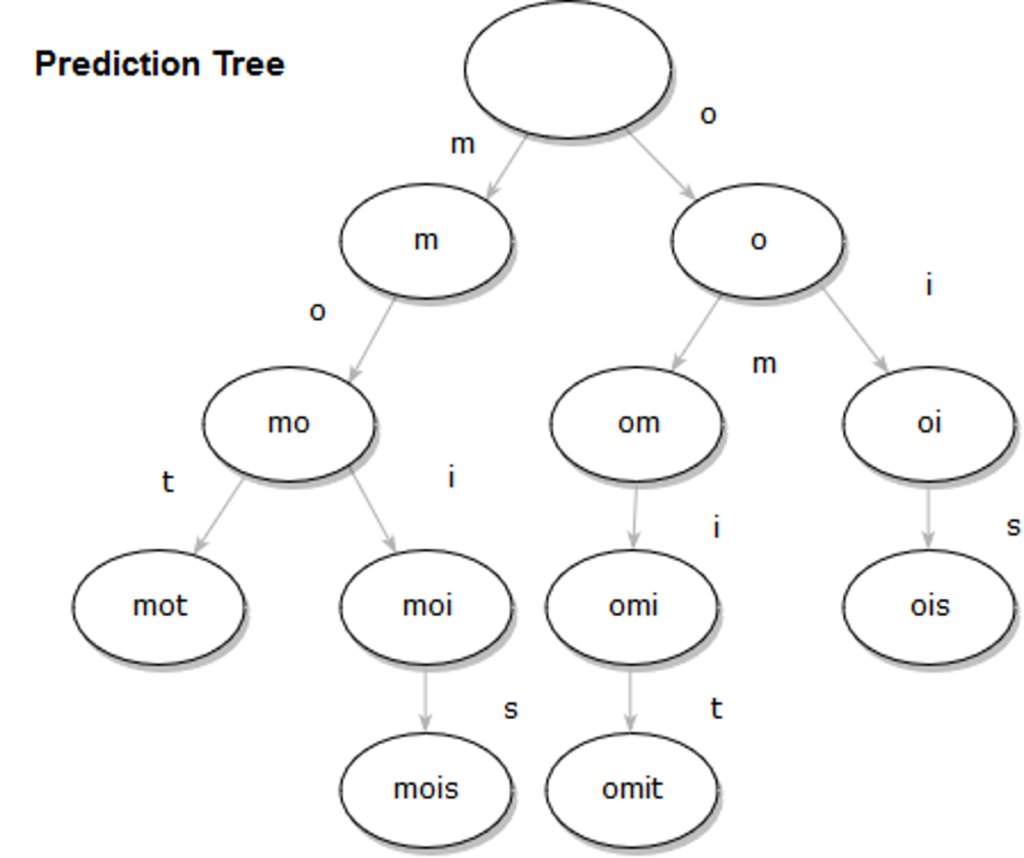
Et voici, une version simple d’un arbre préfixe implémentée en python :
class Trie:
“””
The class Trie, with some methods to insert data and retrieve them
tree = Trie()
node = tree.add_child([0, 1, 2, 1])
Node.retrieve_sequence() # Should return [0, 1, 2, 1]
“””
def __init__(self, parent=None, value = None):
self.children = {} # dict to store children for faster access
self.parent = parent
self.value = value
def add_child(self, values):
“”” Insert reccursively the sequence “values”
“””
value, *sequence_left = values
if value not in self.children: # if the value is not already in the dict, we create a new Node, otherwise we just point to the child and continue the insertion
self.children[value] = Node(self, value)
if sequence_left:
return self.children[value].add_child(sequence_left)
return self.children[value]
def retrieve_sequence(self):
“”” Retrieve all elements stored in the tree from a Node “””
cur = self
retrieved = []
while cur.parent != None:
retrieved.append(cur.value)
cur = cur.parent
return retrieved[::-1]
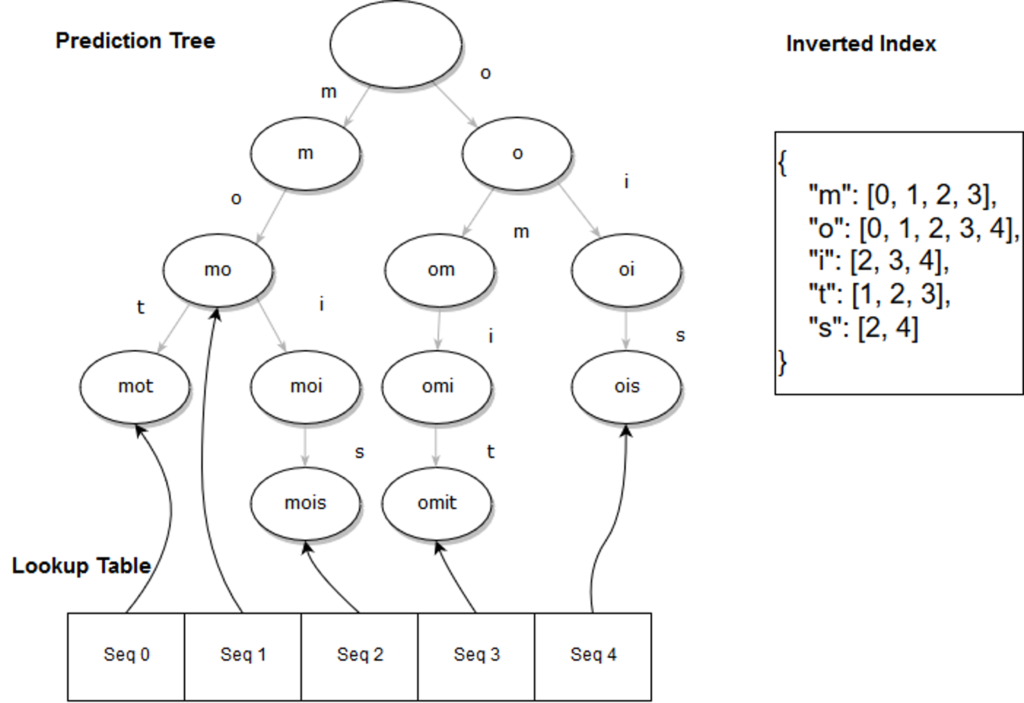
Inverted Index
Pour retrouver rapidement les séquences possédant un élément donné, le Modèle CPT utilise un index inversé (Inverted Index). Il s’agit d’une table de hashage qui, à chaque élément, associe le ou les numéros de séquence dans lesquels l’élément est présent.
Cette table de hashage nous permet ainsi d’accéder en temps constant à l’ensemble des numéros de séquence contenant l’élément. Pour notre exemple avec les séquences suivantes : “mot”, “mo”, “mois”, “omit” et “pos”, on aura cet inverted index :
{
"m": [0, 1, 2, 3], # Car m est présent dans les 4 premières séquences, “mot”, “mo”, “mois”, “omit”
"o": [0, 1, 2, 3, 4],
"i": [2, 3, 4],
"t": [1, 2, 3],
"s": [2, 4]
}
À noter que l’inverted index peut être implémenté via un bitset afin de diminuer au maximum l’empreinte mémoire et d’accélérer certaines opérations (telles que la recherche d’éléments communs entre plusieurs listes/bitset).
Lookup Table
La lookup table permet de retrouver les séquences d’entraînement. C’est une liste dont chaque élément est un pointeur vers le nœud représentant le dernier élément de la séquence d’entraînement correspondante.
En continuant sur notre exemple, voici une représentation complète d’un modèle CPT entraîné :
Entraînement
L’entraînement du modèle CPT s’effectue en complexité temporelle linéaire par rapport au nombre de séquences.
Pour chaque séquence, il suit les trois étapes suivantes :
L’insertion de la séquence dans l’arbre préfixe
L’ajout de chaque élément dans l’inverted index
L’ajout du pointeur du dernier nœud dans la lookup table
Maintenant que nous avons entraîné notre algorithme, voyons comment il peut prédire.
Prédiction
Essayons de prédire quel sera l’élément survenant après la séquence suivante “oi”, appelons cette séquence “séquence cible” par souci de simplicité.
La prédiction s’effectue en 3 étapes :
- Trouver les séquences similaires
- Trouver les séquences résultantes
- Compter les occurrences
Calcul des séquences similaires
Une séquence similaire est une séquence qui contient l’ensemble des éléments de la séquence cible.
Comment cela se passe avec notre Inverted Index ?
L’ensemble des séquences contenant la lettre “o” sont : [0, 1, 2, 3, 4]
L’ensemble des séquences contenant la lettre “i” sont : [2, 3, 4]
Les éléments communs à ces deux listes sont : [2, 3, 4], donc les séquences similaires à notre séquence cible sont les séquences 2, 3 et 4 de notre jeu d’entraînement. C’est-à-dire “mois”, “omit” et “ois”.
Remarque : avec un Bitset, il suffirait de faire des opérations and bit à bit.
Calcul des séquences résultantes
Une séquence résultante est la séquence qui succède au dernier élément en commun entre la séquence similaire et la séquence cible.
Par exemple, si nous avons une séquence cible [“world”, “hello”] avec une séquence similaire [“hello”, “world”, “this”, “is”, “me”], le dernier élément de la séquence similaire en commun avec la séquence cible est “world”, donc la séquence résultante est [“this”, “is”, “me”].
Pour notre exemple, si on calcule les séquences résultantes, cela nous donne :
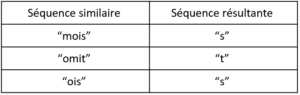
Compter les occurrences
Dans cette dernière étape, nous comptons quels sont les éléments les plus fréquents, ici, la lettre “s”. Donc la prédiction à la suite de la séquence “oi” avec notre jeu d’entraînement est “s”.
Que donne cet algorithme par rapport à d’autres algorithmes state of the art ?
Comparaison par rapport aux autres algorithmes
Framework de test
Pour pouvoir valider les résultats, les auteurs du modèle CPT ont procédé comme suit :
- Chaque séquence est décomposée en trois sous-séquences : le contexte, le préfixe, le suffixe.
- La prédiction est bonne si, en utilisant uniquement le préfixe, on prédit un élément se trouvant dans le suffixe.
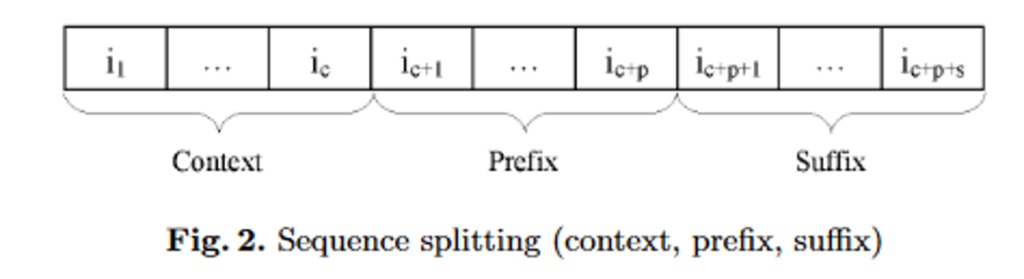
On définit la précision comme étant le nombre de succès divisé par le nombre de prédictions.
Résultats
Les performances du modèle CPT ont été comparées avec les performances des algorithmes “Dependency Graph” (DP), “Prediction by partial matching” (PPM) et “All k order markov” (AKOM).
Les datasets utilisés sont :
- BMS : un historique des pages visitées d’un site e-commerce par session
- FIFA : un historique des pages visitées sur le site FIFA par session en 1998
- SIGN : des séquences de langages de signes retranscrits
- KOSARAK : un historique des pages visitées sur un site de news hongrois
- BIBLE : la Bible, livre religieux chrétien, dont les séquences sont des phrases
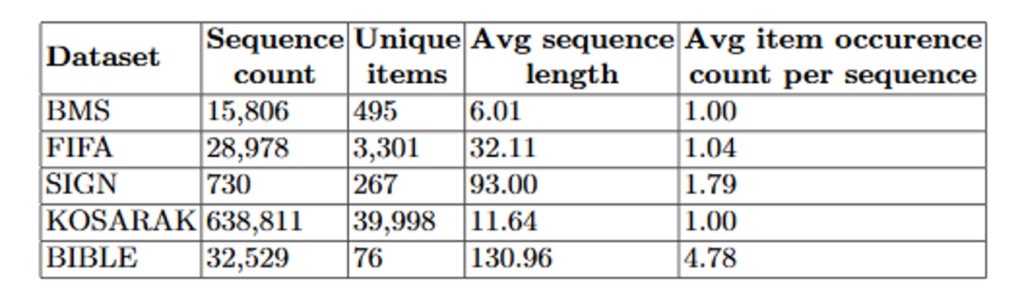
Et voici les résultats selon l’accuracy par dataset et par algorithme :
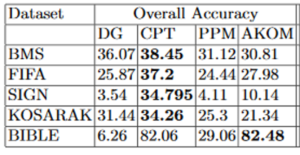
En conclusion, selon le problème et le framework de validation choisis, le modèle CPT peut être un modèle de choix. En plus d’être facilement explicable (contrairement aux réseaux de neurones par exemple), les résultats sont corrects.
En effet, l’accès rapide à l’ensemble des données d’entraînement est un avantage dans certains problèmes. Pour plus de précisions sur l’impact des caractéristiques des jeux de données (nombre de séquences, taille des séquences, etc.) sur la précision, je ne peux que vous conseiller vivement de jeter un coup d’œil sur le benchmark des auteurs.
Un exemple d’implémentation en python
L’algorithme CPT a été développé initialement en Java. Depuis, des implémentations en JavaScript et Python ont vu le jour. Malheureusement, celle en python n’était pas performante. J’ai donc tenté une approche en Cython. Vous pouvez trouver cette approche sur mon github: https://github.com/bluesheeptoken/CPT
Comment l’utiliser ?
Ce package est disponible sur pip, un gestionnaire de paquets pour installer et gérer des paquets Python. Donc un simple « `pip install cpt« ` permet d’installer ce package. Ensuite, il suffit d’importer Cpt, par exemple :
from cpt.cpt import Cpt
model = Cpt()
model.fit([
['hello', 'world'],
['hello', 'this', 'is', 'me'],
['hello', 'me']
])
model.predict([['hello'], ['hello', 'this']])# Output: ['me', 'is']
Pour aller plus loin
Le chercheur Jelte Hoekstra rentre plus dans les détails dans sa thèse sur la prédiction du trafic en heure de pointe dans les transports publics néerlandais.
Le docteur Hoekstra détaille les problématiques des prédictions de séquence et souligne particulièrement bien le fait que le problème premier est de trouver le bon alphabet (ensemble de symboles) pour résoudre le problème. En effet, il faut qu’il soit assez étendu pour que les prédictions aient du sens (dire qu’un utilisateur va prendre le bus au minimum une fois dans le mois n’est pas assez précis). Mais il faut qu’il soit assez étendu pour que les algorithmes puissent comprendre quels sont les comportements similaires. Par exemple, considérer l’heure exacte des prises de bus peut être trompeur, car un voyageur prenant le bus à 8h57 sera traité différemment qu’un voyageur qui prend le bus à 8h58.



Vos commentaires
Je ne comprends pas comment l’inverted index de t est 1,2,3. 2 pour mot, 3 pour omit mais le 1 ?
Merci pour la lecture de l’article !
Effectivement, c’est un erreur, l’inverted index de t devrait être `[0, 3]`. (0 pour « mot », et 3 pour « omit »).
Merci pour le retour je mets à jour rapidement ! 🙂