La recommandation peut se baser sur le principe de similarité: si vous consultez la page d’un portable sur le site, on va probablement vous proposer des portables similaires que celui que vous venez de regarder, la similarité se calcule souvent par rapport à des critères comme le prix, le modèle, la couleur ou les fonctionnalités. Puis une fois que vous avez choisi le portable à acheter, on vous propose ensuite les produits “complémentaires”, par exemple pour le portable que vous avez choisi, on va vous proposer un câble de connexion, un chargeur et une housse. En fait, la complémentarité et la similarité sont deux approches de base du système de recommandation, elles sont appliquées pour des scénarios différents mais partagent toutes les deux le même objectif: trouver les éléments qui correspondent aux intérêts des visiteurs. Pour la recommandation des articles, on s’appuie généralement sur l’approche de similarité, c’est-à-dire trouver les articles du même sujet que celui consulté.
Le Topic Model est une technique de modélisation des documents de texte, en modélisant les documents nous pouvons réinterpréter les textes sous forme mathématique, ce qui nous permet non seulement de calculer la distance des documents, mais aussi de les classifier ou de les regrouper selon nos besoins.
Pourquoi on a besoin du Topic Model?
En pratique, les articles sur un site d’actualité appartiennent toujours à une ou plusieurs catégories, pour les blogs (celui de Meritis par exemple) on a aussi le système de tag qui nous permet de catégoriser les articles. Un système de recommandation brutal doit être capable de proposer au visiteur les articles d’une même catégorie. Mais cette méthode n’est pas toujours efficace, car pour certains sites internet, on ne peut pas créer une hiérarchie trop lourde, cela complique en effet la gestion du site et peut vite noyer les visiteurs lors de la navigation. Un autre problème survient également quand il y a beaucoup d’article dans une même catégorie : comment choisir les articles à recommander puisqu’on ne connait pas le poids de chaque article dans la catégorie ? Dans ce genre de situations, la description des catégories doit donc rester assez générale et relativement simple réduisant par conséquent la précision d’une recommandation brutale basée uniquement sur la catégorie.
Nous nous intéresserons donc dans cet article aux moyens d’identifier automatiquement le sujet d’un article et de comprendre le contenu d’un article de manière sémantique indépendamment de la structure du site.
Pour résoudre cette problématique, les Data Scientists ont introduit les algorithmes “Topic Model”: il s’agit de modéliser les articles (ou de manière plus générale, les documents de texte) pour déterminer le sujet abstrait des documents, en utilisant des moyens probabilistes. La plupart des algorithmes de Topic model sont non-supervisés, ce qui signifie qu’on n’a pas besoin de définir les classes avant l’apprentissage, l’algorithme associe automatiquement les documents par groupe en fonction de leur similarité. Pour certains cas particuliers où on souhaite que l’algorithme donne clairement la catégorie de l’article, on peut rajouter un classificateur à la sortie de Topic Model (dans ce cas, Topic Model est utilisé comme un extracteur de features). Il existe également des Topic Models évolutionnaires spécifiquement conçus pour l’apprentissage supervisé.
Distribution Binomial et Distribution Multinomial
Si on veut écrire un article qui présente le marché du paiement mobile, on va surement parler de différents sujets (ou topics) comme la banque, le smartphone et le paiement. Pour le topic “banque”, les mots “agence bancaire”, “crédit”, “frais” seront utilisés plus fréquemment. De même, pour le topic “smartphone”, on voit souvent les mots “ios”, “android”, “iphone”, “processeur”, “facilité”. Puis pour le topic “paiement”, on utilisera souvent les mots comme “sécurité”, “montant”, “carte bancaire”, “sans contact”, “commerçant”… On peut donc voir que pour un article avec un sujet général donné, certains topics seront plus parlés que les autres, et pour chaque topic, certains mots auront plus de chance d’être employés que les autres, il existe donc une relation probabiliste entre le mot, le topic et le document:
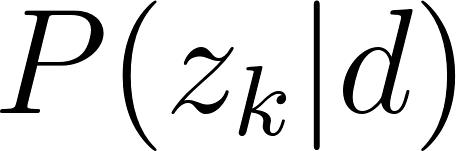 : la probabilité de topic
: la probabilité de topic 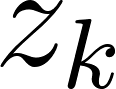 dans le document
dans le document 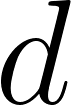 ;
;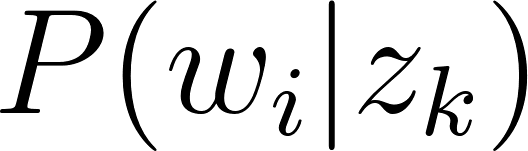 : la probabilité de mot
: la probabilité de mot 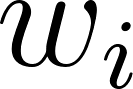 dans le topic
dans le topic 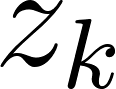 ;
;
En parlant de probabilité, vous avez probablement déjà joué au jeu “pile ou face”. En jetant une pièce de monnaie en l’air, on a 50% de chance d’avoir pile et 50% de chance d’obtenir face. Si on jette cette monnaie 5 fois, quelle est la probabilité d’avoir 3 fois pile et 2 fois face?
Il y a 10 cas possibles:
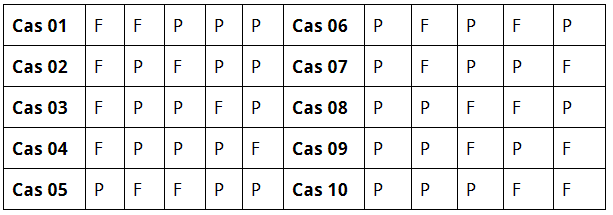
Dans chaque cas, la probabilité est égale à ![]() , comme il y a en total 10 cas possibles, la probabilité totale est de
, comme il y a en total 10 cas possibles, la probabilité totale est de ![]() , il y a donc 31,5% de probabilité d’avoir 3 fois pile si on jette une pièce de monnaie 5 fois.
, il y a donc 31,5% de probabilité d’avoir 3 fois pile si on jette une pièce de monnaie 5 fois.
Plus généralement, si la probabilité de succès est ![]() , en répétant
, en répétant ![]() fois le jeu, la probabilité d’avoir
fois le jeu, la probabilité d’avoir ![]() fois succès est:
fois succès est:
![]() (1)
(1)
![]() est le coefficient binomial, parfois on utilise aussi
est le coefficient binomial, parfois on utilise aussi ![]() .
. ![]() (dans l’exemple,
(dans l’exemple, ![]() ). Mathématiquement, le jeu de “pile ou face” est en effet une épreuve de Bernoulli, qui est une série d’expérimentation avec le résultat “succès” ou “échec”, la distribution de probabilité dans ce cas est appelé “distribution binomiale”.
). Mathématiquement, le jeu de “pile ou face” est en effet une épreuve de Bernoulli, qui est une série d’expérimentation avec le résultat “succès” ou “échec”, la distribution de probabilité dans ce cas est appelé “distribution binomiale”.
Si on remplace la pièce de monnaie par un dé,: au lieu de “pile” et “face”, on a 6 possibilités 1, 2, 3, 4, 5, 6. La probabilité dans ce cas est égale à:
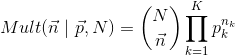 (2)
(2)
Si ![]() résultats sont possibles à chaque expérimentation, la distribution de probabilité suit la loi Multinomiale. La Distribution Binomiale est effectivement le cas particulier de la Distribution Multinomiale si
résultats sont possibles à chaque expérimentation, la distribution de probabilité suit la loi Multinomiale. La Distribution Binomiale est effectivement le cas particulier de la Distribution Multinomiale si ![]() :
:
![]() (3)
(3)
Si vous avez compris le principe de la distribution multinomiale, le topic model n’est pas plus difficile. Imaginons que le document de texte est une séquence des mots:
![]()
Dans le contexte de topic model, l’ordre des mots est ignoré, car on peut supposer que les mots dans la phrase sont déterminés par la grammaire, et l’ordre des phrases a très peu d’impact sur la compréhension sémantique de l’article.
Un document peut ensuite être exprimé sous la forme suivante:
![]()
Où ![]() est le mot dans le document avec
est le mot dans le document avec ![]() sa fréquence dans le document. On considère que le corpus peut être décrit au moyen d’un dictionnaire (des « mots »). Un document particulier est représenté par l’histogramme des occurrences des mots le composant, une telle description s’appelle “bag-of-words” (sac de mots). Dit autrement, supposons qu’il y a un dé avec
sa fréquence dans le document. On considère que le corpus peut être décrit au moyen d’un dictionnaire (des « mots »). Un document particulier est représenté par l’histogramme des occurrences des mots le composant, une telle description s’appelle “bag-of-words” (sac de mots). Dit autrement, supposons qu’il y a un dé avec ![]() faces, la génération d’un document particulier peut être considérée comme le jeu de ce dé, qui suit également la loi multinomiale, sauf qu’on ne connaît pas la densité de dé, c’est-à-dire la probabilité de chaque face. Mais comme on sait que cette probabilité est en quelque sorte reliée au sujet du document, en estimant la probabilité, on trouvera le sujet du document.
faces, la génération d’un document particulier peut être considérée comme le jeu de ce dé, qui suit également la loi multinomiale, sauf qu’on ne connaît pas la densité de dé, c’est-à-dire la probabilité de chaque face. Mais comme on sait que cette probabilité est en quelque sorte reliée au sujet du document, en estimant la probabilité, on trouvera le sujet du document.
Estimation du Maximum de Vraisemblance
Dans la section précédente, on a présenté le modèle bag-of-words, dans ce modèle, la génération de document de texte suit la loi multinomiale, la détermination du sujet de document peut se transférer à la problématique de l’estimation de probabilité de mot.
Pour simplifier la compréhension, on commence par le cas binomial. Rappelons d’abord la Distribution Binomiale :
![]() (1)
(1)
Dans l’équation (1), les paramètres ![]() et
et ![]() sont connus, comme pour une pièce de monnaie, on sait que
sont connus, comme pour une pièce de monnaie, on sait que ![]() et
et ![]() le nombre total de jet. Dans la théorie de la probabilité, on dit que
le nombre total de jet. Dans la théorie de la probabilité, on dit que ![]() est une probabilité conditionnelle, ce qui signifie la probabilité d’événement (
est une probabilité conditionnelle, ce qui signifie la probabilité d’événement (![]() fois “pile” pour
fois “pile” pour ![]() jet) sachant
jet) sachant ![]() et
et ![]() . Dans le cas de topic model, comme
. Dans le cas de topic model, comme ![]() est inconnu, l’événement
est inconnu, l’événement ![]() constitue les documents qui sont observés, l’équation devient:
constitue les documents qui sont observés, l’équation devient:
![]() (3)
(3)
L’équation (3) est appelée la fonction de vraisemblance (en anglais, likelihood function), c’est important de comprendre la différence entre la vraisemblance et la probabilité. La probabilité décrit la possibilité d’événement ![]() sachant
sachant ![]() , alors que la vraisemblance décrit la possibilité de valeur
, alors que la vraisemblance décrit la possibilité de valeur ![]() sachant l’événement
sachant l’événement ![]() . Pour distinguer, on utilise
. Pour distinguer, on utilise ![]() (
(![]() comme likelihood) au lieu de
comme likelihood) au lieu de ![]() , le bon estimateur de
, le bon estimateur de ![]() est celui qui peut maximiser la vraisemblance. Dans l’équation, le terme
est celui qui peut maximiser la vraisemblance. Dans l’équation, le terme ![]() est constant, on cherche donc l’estimateur
est constant, on cherche donc l’estimateur ![]() qui maximise:
qui maximise:
![]() (4)
(4)
Si ![]() ,
, ![]()
Si ![]() ,
, ![]()
Si ![]() ,
, ![]()
Si ![]() ,
, ![]()
D’après le calcul, on voit que si on obtient 3 fois pile sur 5 jets, ![]() est plus vraisemblable que
est plus vraisemblable que ![]() . En fait, il est facile de prouver que la fonction de vraisemblance atteint la valeur maximum lorsque
. En fait, il est facile de prouver que la fonction de vraisemblance atteint la valeur maximum lorsque ![]() , on l’appelle l’estimation du maximum de vraisemblance. Malgré sa notion mathématique, on voit que cette estimation est assez naturelle.
, on l’appelle l’estimation du maximum de vraisemblance. Malgré sa notion mathématique, on voit que cette estimation est assez naturelle.
En statistique, l’estimation de vraisemblance est approuvée par le fréquentiste, qui considère que la probabilité a une valeur inconnue mais certaine, on cherche à trouver un moyen qui nous permet de trouver la meilleur estimation de la probabilité. Mais d’autres statisticiens considèrent que la probabilité n’est pas une valeur constante, selon l’événement observé, la probabilité suit elle-même une distribution, autrement dit, ils cherchent à déterminer “la probabilité de probabilité”: On a d’abord une distribution de probabilité a priori, puis selon l’événement observé, on ajuste cette distribution au fur et à mesure. On appelle ce dernier le bayésien.
Dans cet article, on ne discute pas quelle approche est meilleure, en fait, il n’y a pas de bonne ou mauvaise approche. Mais pour l’étude du Topic Model, on préfère utiliser la statistique bayésienne, puisque la probabilité des mots peut varier en fonction de l’habitude des auteurs, c’est mieux de considérer l’ensemble de probabilité possible plutôt que de choisir une seule “meilleure estimation”.
Distribution Beta et Distribution Dirichlet
Imaginez que vous êtes manager d’une équipe de baseball, et que vous voulez estimer la moyenne à la batte pour un joueur de votre équipe. Vous pourriez dire que nous pouvons simplement utiliser sa moyenne à la batte jusqu’à présent, puis utiliser ![]() qui est l’estimation du maximum de vraisemblance, mais ce serait une mauvaise estimation si on est au début d’une saison. Si un frappeur n’est présent qu’une fois à la batte et obtient un coup sûr, sa moyenne à la batte est 1,000 tandis que s’il est retiré sur 3 prises sa moyenne à la batte est de 0,000. L’estimation ne sera pas mieux même si vous avez les données de 5 ou 6 matchs: si le frappeur a une série chanceuse d’obtenir une moyenne de 1,000 ou une série malchanceuse en obtenant une moyenne de 0 aucune n’est le bon estimateur pour la performance de la saison.
qui est l’estimation du maximum de vraisemblance, mais ce serait une mauvaise estimation si on est au début d’une saison. Si un frappeur n’est présent qu’une fois à la batte et obtient un coup sûr, sa moyenne à la batte est 1,000 tandis que s’il est retiré sur 3 prises sa moyenne à la batte est de 0,000. L’estimation ne sera pas mieux même si vous avez les données de 5 ou 6 matchs: si le frappeur a une série chanceuse d’obtenir une moyenne de 1,000 ou une série malchanceuse en obtenant une moyenne de 0 aucune n’est le bon estimateur pour la performance de la saison.
En effet, si le frappeur est retiré sur 3 prises, personne ne dira qu’il n’obtiendra jamais un coup pour toute la saison. Parce qu’on a l’expérience antérieure. Nous savons que dans l’histoire, la plupart des moyennes à la batte au cours d’une saison ont oscillé entre 0,215 et 0,360. Nous savons que si un joueur obtient quelques retraits à la batte au début, cela pourrait indiquer qu’il se retrouvera un peu moins bon que la moyenne, mais nous savons qu’il ne déviera probablement pas de cette fourchette.
Le problème de moyenne à la batte est aussi une distribution binomiale (une série de succès et d’échecs). Avant le premier coup du frappeur, on estime que sa moyenne à la batte sera entre 0,215 et 0,360. L’estimation est basée sur notre expérience antérieure, qui est représentée par la distribution bêta. Le domaine de distribution bêta est [0, 1], tout comme une probabilité.
La distribution bêta peut s’écrire :
![]() (5)
(5)
On ne va pas rentrer dans le détail de cette distribution, pour le moment, tout ce qu’on a besoin de savoir, c’est que dans la distribution bêta, on a les paramètres ![]() qui peuvent influencer la forme de la distribution:
qui peuvent influencer la forme de la distribution:
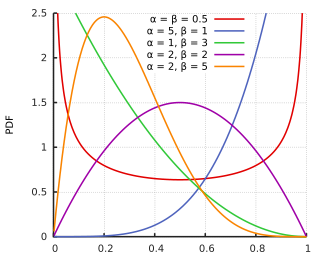
Sachant les valeurs des paramètres ![]() et
et ![]() , l’espérance mathématique de Distribution Bêta est:
, l’espérance mathématique de Distribution Bêta est:
![]()
Revenons sur l’exemple du baseball, comme nous savons déjà que pour une saison, la moyenne à la batte des frappeurs varie entre 0,215 et 0,360 avec une moyenne autour de 0,27 on va mettre ![]() et
et ![]() qui donnent la distribution suivante:
qui donnent la distribution suivante:
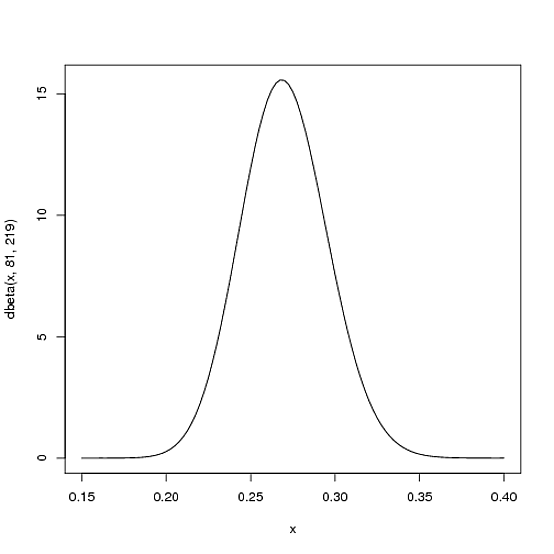
Comme vous voyez, cette distribution correspond bien à notre attente car elle a une moyenne autour de 0,27 et s’arrête à 0,20 et 0,35 à chaque côté. Dans le schéma, l’axe ![]() représente la moyenne à la batte du frappeur, qui est la probabilité d’obtenir un coup sûr, l’axe
représente la moyenne à la batte du frappeur, qui est la probabilité d’obtenir un coup sûr, l’axe ![]() est la confiance de la moyenne à la batte correspondante, ce dernier est en effet aussi une probabilité, qui décrit la sûreté la moyenne à la batte à l’axe
est la confiance de la moyenne à la batte correspondante, ce dernier est en effet aussi une probabilité, qui décrit la sûreté la moyenne à la batte à l’axe ![]() . On peut considérer que la distribution bêta est “la probabilité de probabilité”.
. On peut considérer que la distribution bêta est “la probabilité de probabilité”.
Maintenant le frappeur a fait un coup, nous devons ensuite mettre à jour nos probabilités: nous voulons déplacer la courbe un peu pour refléter les nouvelles informations arrivées. La nouvelle distribution Bêta sera:
![]()
La nouvelle courbe de distribution est donc:
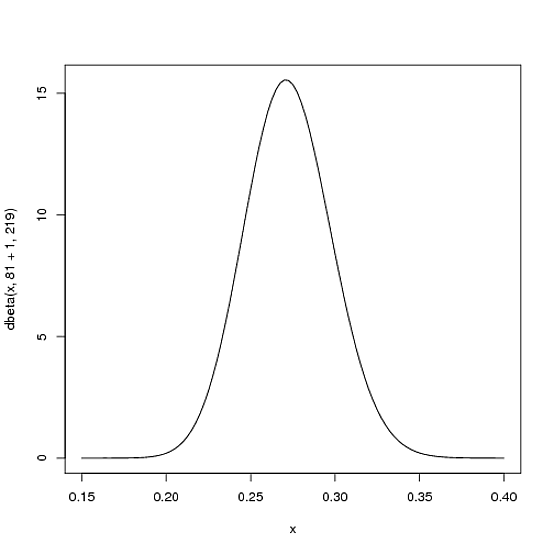
On ne voit pas une grande différence dans la nouvelle courbe, cela reflète en fait la réalité: on ne juge pas la performance du jour par un seul coup.
Supposons qu’à la moitié de saison, le frappeur arrive à faire 100 coups, en ratant 200 fois, la nouvelle distribution bêta sera ![]() :
:
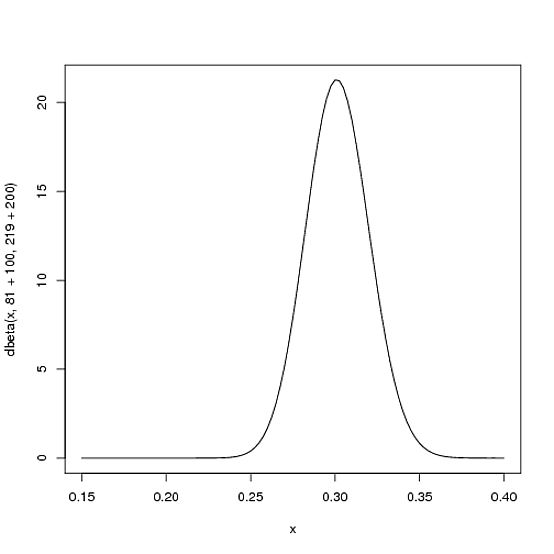
Notez que maintenant la courbe est à la fois plus fine et décalée vers la droite (moyenne à la batte plus élevée). Rappelons que la moyenne de la distribution Bêta est ![]() , la moyenne de bêta distribution à la moitié de saison est donc
, la moyenne de bêta distribution à la moitié de saison est donc ![]() , cette valeur est moins élevée que l’estimation de vraisemblance qui est de
, cette valeur est moins élevée que l’estimation de vraisemblance qui est de ![]() mais plus élevée que la moyenne au début de saison qui est de
mais plus élevée que la moyenne au début de saison qui est de ![]() .
.
Cette nouvelle estimation est appelée “inférence bayésienne”, qui est initialisée par une distribution a priori (dans l’exemple, on a utilisé la bêta distribution avec ![]() et
et ![]() ), la distribution a priori est ajustée par les nouvelles informations arrivées:
), la distribution a priori est ajustée par les nouvelles informations arrivées:
![]() (6)
(6)
Tout comme la Distribution Multinomial qui est le cas général de la Distribution Binomial, la Distribution Bêta a aussi sa version en hautes dimensions, la Distribution Dirichlet:
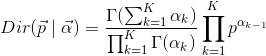 (7)
(7)
Avec:
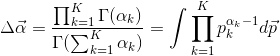 (8)
(8)
Si on compare la Distribution Dirichlet (7) à la Distribution Bêta (5), on peut trouver que les deux fonctions sont de même forme, sauf que dans la Distribution Bêta, il n’y a que 2 paramètres ![]() et
et ![]() , et 2 probabilités
, et 2 probabilités ![]() et
et ![]() , Dans le cas Dirichlet, le paramètre
, Dans le cas Dirichlet, le paramètre ![]() et la probabilité
et la probabilité ![]() sont deux vecteurs de
sont deux vecteurs de ![]() dimensions.
dimensions.
LDA (Latent Dirichlet Allocation)
Après avoir compris le contexte mathématique de Topic Model, on peut maintenant revenir sur notre sujet principal, c’est-à-dire sachant un corpus donné (ensemble des documents de texte), comment calculer la distribution de topic ainsi que la distribution de mots pour chaque topic.
Comme vous voyez, les mots dans le document de texte, décrits par le modèle bag-of-words, suivent essentiellement la Distribution Multinomiale, cette dernière peut se calculer à partir de sa distribution a priori conjuguée: la Distribution Dirichlet.
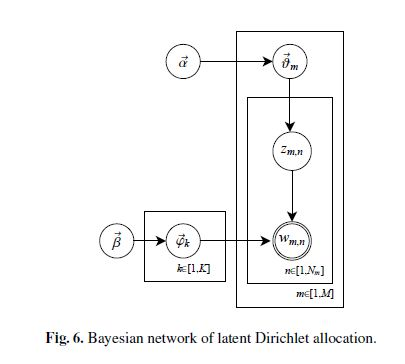
En ignorant l’ordre des mots, le processus de LDA peut se générer de manière suivante:
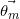 est la distribution des topics qui suit la loi multinomiale,
est la distribution des topics qui suit la loi multinomiale, 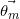 a
a 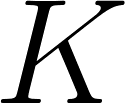 dimensions où
dimensions où 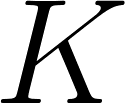 est le nombre de topics dans le corpus;
est le nombre de topics dans le corpus;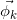 est la distribution des mots pour le topic de l’index
est la distribution des mots pour le topic de l’index 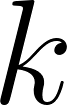 qui suit la loi multinomiale,
qui suit la loi multinomiale, 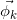 a
a 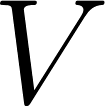 dimensions où
dimensions où 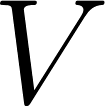 est le nombre de termes dans le bag-of-word;
est le nombre de termes dans le bag-of-word;- Pour le document
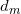 parmi les
parmi les 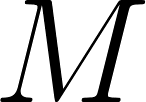 documents de corpus, on va d’abord échantillonner l’index du topic
documents de corpus, on va d’abord échantillonner l’index du topic 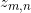 , qui est le numéro de topic du
, qui est le numéro de topic du 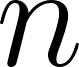 ème mot dans le document
ème mot dans le document 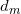 ,
, 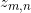 est une valeur comprise entre 1 et
est une valeur comprise entre 1 et 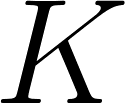 ;
; - A partir de
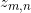 , choisir la distribution
, choisir la distribution 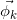 correspondant et échantillonner le mot
correspondant et échantillonner le mot 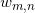 ,
, 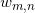 est le
est le 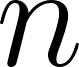 ème mot dans le document
ème mot dans le document 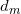
En pratique, on s’intéresse au processus de sens inverse: Étant donné le corpus et le nombre de topic ![]() , comment estimer
, comment estimer ![]() et
et ![]() , , rappelons que le topic peut s’exprimer par une relation probabiliste des mots, en estimant
, , rappelons que le topic peut s’exprimer par une relation probabiliste des mots, en estimant ![]() et
et ![]() , on peut trouver les topics dans les documents.
, on peut trouver les topics dans les documents. ![]() et
et ![]() sont deux distributions qu’on ne peut observer directement, comme elles sont toutes des distributions Multinomiales, on va utiliser la Distribution Dirichlet
sont deux distributions qu’on ne peut observer directement, comme elles sont toutes des distributions Multinomiales, on va utiliser la Distribution Dirichlet ![]() et
et ![]() pour les estimer.
pour les estimer.
Gibbs Sampling
Bien que le principe du modèle LDA soit relativement simple, ![]() et
et ![]() ne sont pas si facile à estimer, En pratique, on est obligé d’utiliser l’analyse numérique pour résoudre les équations. Dans Latent Dirichlet Allocation, Blei, David M.; Ng, Andrew Y.; Jordan, Michael, 2002, la méthode EM (Expectation–maximization) a été introduite pour le calcul de
ne sont pas si facile à estimer, En pratique, on est obligé d’utiliser l’analyse numérique pour résoudre les équations. Dans Latent Dirichlet Allocation, Blei, David M.; Ng, Andrew Y.; Jordan, Michael, 2002, la méthode EM (Expectation–maximization) a été introduite pour le calcul de ![]() et
et ![]() , puis dans Gibbs sampling in the generative model of latent dirichlet allocation, T Griffiths, 2002, la méthode Gibbs sampling a été utilisé, ce dernier étant plus rapide et plus facile à paralléliser.
, puis dans Gibbs sampling in the generative model of latent dirichlet allocation, T Griffiths, 2002, la méthode Gibbs sampling a été utilisé, ce dernier étant plus rapide et plus facile à paralléliser.
Gibbs Sampling est un algorithme de la famille MCMC (Markov chain Monte Carlo). Lorsqu’on traite une distribution inconnue ou trop complexe pour obtenir la solution analytique, on utilise la méthode MCMC afin d’échantillonner la distribution. En obtenant l’échantillon de la distribution, on arrive à identifier la structure de la distribution.
Dans cet article, on ne présentera pas le détail mathématique de Gibbs Sampling ou MCMC, en général, Gibbs Sampling a besoin de la distribution jointe des mots et des topics pour la génération de l’échantillon.
Notons ![]() la distribution jointe:
la distribution jointe:
![]() (11)
(11)
Correspondant au processus de génération de corpus présentée dans la section précédente, ![]() est la génération du topic, et
est la génération du topic, et ![]() la génération du mot.
la génération du mot.
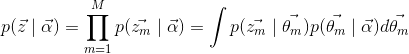 (12)
(12)
avec l’équation (7) et (8), on a la probabilité document-topic:
![]() (12)
(12)
De même façon, on peut calculer la probabilité topic-mot:
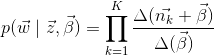 (13)
(13)
Avec l’équation (12) et (13), on a la distribution jointe:
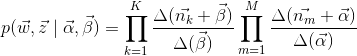 (14)
(14)
Avec la distribution jointe, Gibbs Sampling peut générer l’échantillon ![]() correspondant, à partir de l’échantillon, on peut calculer
correspondant, à partir de l’échantillon, on peut calculer ![]() et
et ![]() , qui sont la distribution posteriori de
, qui sont la distribution posteriori de ![]() et
et ![]() . En fait, le paramètre
. En fait, le paramètre ![]() est lié au document dans le corpus (données d’apprentissage), qui est inutile pour la compréhension des nouveaux documents, donc en pratique, il n’est pas nécessaire de conserver
est lié au document dans le corpus (données d’apprentissage), qui est inutile pour la compréhension des nouveaux documents, donc en pratique, il n’est pas nécessaire de conserver ![]() pour le modèle LDA entraîné. En général, afin d’améliorer la qualité du modèle, lors de l’apprentissage du modèle LDA, nous prenons souvent la moyenne des résultats de n itérations après la convergence de Gibbs Sampling pour faire l’estimation des paramètres.
pour le modèle LDA entraîné. En général, afin d’améliorer la qualité du modèle, lors de l’apprentissage du modèle LDA, nous prenons souvent la moyenne des résultats de n itérations après la convergence de Gibbs Sampling pour faire l’estimation des paramètres.
Conclusion
En introduisant Latent Dirichlet Allocation, nous avons maintenant une vue générale sur le Topic Model. LDA est un algorithme qui est relativement simple à implémenter, mais pour le comprendre, il faut une forte connaissance en statistique, y compris l’inférence bayésienne, la distribution multinomiale, la distribution dirichlet ainsi que le markov chain et la simulation Monte-Carlo. Cet article a donc abordé la présentation d’un algorithme de Machine Learning mais aussi l’introduction des principes de statistique concernés.
LDA est un algorithme classique de Topic Model, depuis sa première apparence en 2002, on a aujourd’hui plusieurs modèles évolutionnaires pour traiter des différents cas particuliers, mais ils partagent tous la même théorie que LDA.
LDA nous permet d’évaluer la distribution de topic du document de texte, le output d’algorithme est donc souvent en format d’un vecteur de probabilité, en pratique, on peut utiliser ce dernier pour calculer la similarité des documents, ou les classifier.




Vos commentaires
excellent article, Merci pour l’effort et le partage.
excelllent article